搜索环境
静态环境:搜索结构在执行插入和删除等操作的前后不发生变化。这种结构操作简单,效率不高,而且需要处理一出问题。
动态环境:为了保持较高的搜索效率,搜索结构在执行插入和删除等操作的前后将自动进行调整,结构可能会发生变化
前者称为静态搜索结构,后者称为动态搜索结构。
二叉搜索树
折半查找,每次从搜索序列的中间进行搜索,把区间缩小一半,通过有限次的迭代,很快就能逼近到所要寻找的元素。如果我们直接输入搜索序列,构造出类似于折半搜索的判定树那样的树形结构,就能实现快速搜索。这种树形结构就是二叉搜索树。
二叉搜索树的概念
二叉搜索树是一棵空树,或是具有下列性质的树:
1. 每个结点都有一个作为搜索依据的关键码(key),所有结点的关键码互不相同
2. 左子树(如果存在)上所有结点的关键码都小于根结点的关键码
3. 右子树(如果存在)上所有结点的关键码都大于根结点的关键码
4. 左子树和右子树也是二叉搜索树
关键码事实上是结点所保存元素中某个域的值,它能够唯一的表示这个节点。因此,如果对一棵二叉搜索树进行中序遍历,可以按从小到大的顺序,将各个结点关键码排列起来,所以也成二叉搜索树为二叉排序树。
二叉搜索树上的搜索
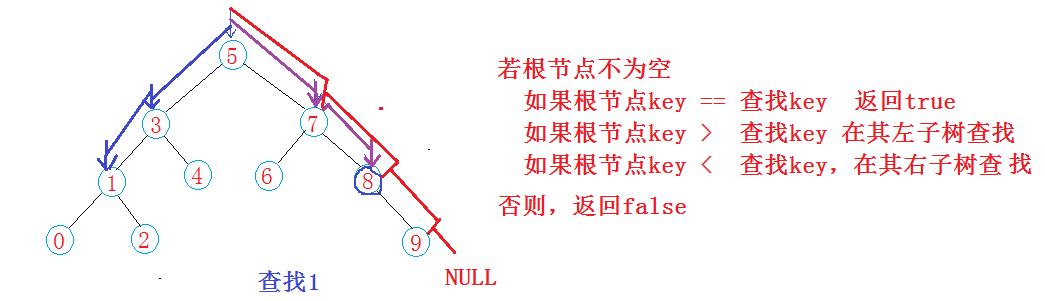
二叉树的插入
- 比结点大的插入到结点的右子树
- 比结点小的插入到结点的左子树
- 与已有结点相同的值不进行插入
二叉树的删除
在二叉树中删除一个结点时,必须将因结点删除而断开的二叉链表重新连接起来,同时确保二叉搜索树的性质不会失去。此外,为了保证在执行删除后树的性能不至于降低,还需要防止重新链接后树的高度不能增加。
在判断需要删除的结点时,有以下情况:
- 要删除的结点无孩子结点
- 要删除的结点只有左孩子结点
- 要删除的结点只有右孩子结点
- 要删除的结点有左、右孩子结点
情况1可以归类到2或者3
对于上述情况,相应的删除方法如下:
a、直接删除该结点
b、删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点;
c、删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点;
d、在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,在来处理该结点的删除问题
代码实现
#include<stdio.h>
#include<iostream>
using namespace std;
template<class T>
struct BSTNode
{
BSTNode<T> * _pLeft; // 左孩子
BSTNode<T> * _pRight; // 右孩子
T _data; // 数据域
// 构造函数
BSTNode()
:_pLeft(NULL)
, _pRight(NULL)
{}
// 构造函数
BSTNode(const T x)
{
_data = x;
_pLeft = NULL;
_pRight = NULL;
}
};
template<class T>
class BST
{
public:
// 构造函数
BST()
:_pRoot(NULL)
{}
// 构造函数
BST(const T * arr, size_t size)
{
for (int i = ; i < size; i++)
Insert(arr[i],root);
}
// 析构函数
~BST()
{
makeEmpty(_pRoot);
}
// 插入函数
bool Insert(const T n)
{
return Insert(n, _pRoot);
}
// 搜索函数
bool Search(const T n)
{
return Search(n, _pRoot);
}
// 删除函数
bool Remove(const T n)
{
return Remove(n, _pRoot);
}
// 显示二叉树
void printTree()const
{
printTree(_pRoot);
}
private:
BSTNode<T> * _pRoot; // 二叉树根指针
// 置空函数
void makeEmpty(BSTNode<T> * ptr)
{
if (ptr == NULL)
return;
makeEmpty(ptr->_pLeft);
makeEmpty(ptr->_pRight);
delete ptr;
}
// 插入函数
bool Insert(const T n, BSTNode<T> *& ptr)
{
if (ptr == NULL)
{
ptr = new BSTNode<T>(n);
if (ptr == NULL)
cout << "内存分配错误!" << endl;
return false;
}
else if (n < ptr->_data)
Insert(n, ptr->_pLeft);
else if (n > ptr->_data)
Insert(n, ptr->_pRight);
else
{
cout << "数据已存在!" << endl;
return false;
}
return true;
}
// 搜索函数
bool Search(const T n, BSTNode<T> * ptr)
{
while (ptr)
{
if (ptr->_data == n)
return true;
else if (ptr->_data < n)
ptr = ptr->_pRight;
else
ptr = ptr->_pLeft;
}
cout << "内容不存在!" << endl;
return false;
}
// 删除函数
bool Remove(const T n, BSTNode<T> *& ptr)
{
BSTNode<T> * del; // 删除的结点
if (ptr == NULL)
{
cout << "数据为空!" << endl;
return false;
}
if (ptr->_data == n)
{
// 左右子女均存在的情况
if (ptr->_pLeft != NULL && ptr->_pRight != NULL)
{
del = ptr->_pRight;
while (del->_pLeft != NULL)
del = del->_pLeft;
ptr->_data = del->_data;
Remove(del->_data, ptr->_pRight);
}
else
{
del = ptr;
/*if (ptr->_pLeft != NULL)
ptr = ptr->_pLeft;
else if (ptr->_pRight != NULL)
ptr = ptr->_pRight;
else
ptr = NULL;*/
if (ptr->_pRight != NULL)
ptr = ptr->_pRight;
else
ptr = ptr->_pLeft;
delete del;
return true;
}
}
else if (ptr->_data > n)
Remove(n, ptr->_pLeft);
else if (ptr->_data < n)
Remove(n, ptr->_pRight);
}
// 显示输出函数
bool printTree(BSTNode<T> * ptr)const
{
if (ptr == NULL)
return false;
printTree(ptr->_pLeft);
cout << ptr->_data << " ";
printTree(ptr->_pRight);
}
};
int main()
{
BST<int> s;
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Remove();
s.printTree();
return ;
}