搜尋環境
靜态環境:搜尋結構在執行插入和删除等操作的前後不發生變化。這種結構操作簡單,效率不高,而且需要處理一出問題。
動态環境:為了保持較高的搜尋效率,搜尋結構在執行插入和删除等操作的前後将自動進行調整,結構可能會發生變化
前者稱為靜态搜尋結構,後者稱為動态搜尋結構。
二叉搜尋樹
折半查找,每次從搜尋序列的中間進行搜尋,把區間縮小一半,通過有限次的疊代,很快就能逼近到所要尋找的元素。如果我們直接輸入搜尋序列,構造出類似于折半搜尋的判定樹那樣的樹形結構,就能實作快速搜尋。這種樹形結構就是二叉搜尋樹。
二叉搜尋樹的概念
二叉搜尋樹是一棵空樹,或是具有下列性質的樹:
1. 每個結點都有一個作為搜尋依據的關鍵碼(key),所有結點的關鍵碼互不相同
2. 左子樹(如果存在)上所有結點的關鍵碼都小于根結點的關鍵碼
3. 右子樹(如果存在)上所有結點的關鍵碼都大于根結點的關鍵碼
4. 左子樹和右子樹也是二叉搜尋樹
關鍵碼事實上是結點所儲存元素中某個域的值,它能夠唯一的表示這個節點。是以,如果對一棵二叉搜尋樹進行中序周遊,可以按從小到大的順序,将各個結點關鍵碼排列起來,是以也成二叉搜尋樹為二叉排序樹。
二叉搜尋樹上的搜尋
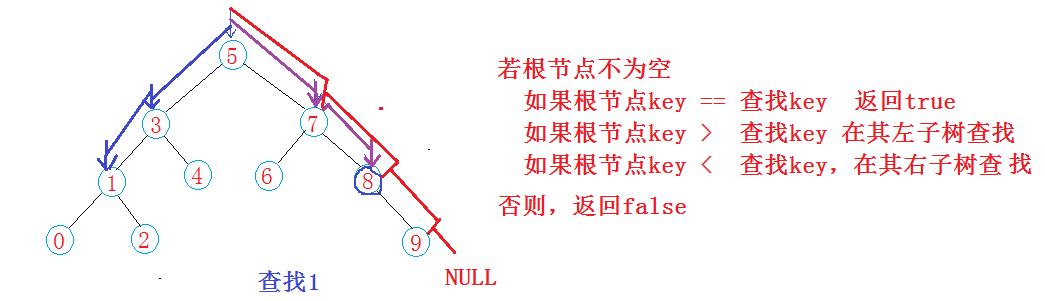
二叉樹的插入
- 比結點大的插入到結點的右子樹
- 比結點小的插入到結點的左子樹
- 與已有結點相同的值不進行插入
二叉樹的删除
在二叉樹中删除一個結點時,必須将因結點删除而斷開的二叉連結清單重新連接配接起來,同時確定二叉搜尋樹的性質不會失去。此外,為了保證在執行删除後樹的性能不至于降低,還需要防止重新連結後樹的高度不能增加。
在判斷需要删除的結點時,有以下情況:
- 要删除的結點無孩子結點
- 要删除的結點隻有左孩子結點
- 要删除的結點隻有右孩子結點
- 要删除的結點有左、右孩子結點
情況1可以歸類到2或者3
對于上述情況,相應的删除方法如下:
a、直接删除該結點
b、删除該結點且使被删除節點的雙親結點指向被删除節點的左孩子結點;
c、删除該結點且使被删除節點的雙親結點指向被删除結點的右孩子結點;
d、在它的右子樹中尋找中序下的第一個結點(關鍵碼最小),用它的值填補到被删除節點中,在來處理該結點的删除問題
代碼實作
#include<stdio.h>
#include<iostream>
using namespace std;
template<class T>
struct BSTNode
{
BSTNode<T> * _pLeft; // 左孩子
BSTNode<T> * _pRight; // 右孩子
T _data; // 資料域
// 構造函數
BSTNode()
:_pLeft(NULL)
, _pRight(NULL)
{}
// 構造函數
BSTNode(const T x)
{
_data = x;
_pLeft = NULL;
_pRight = NULL;
}
};
template<class T>
class BST
{
public:
// 構造函數
BST()
:_pRoot(NULL)
{}
// 構造函數
BST(const T * arr, size_t size)
{
for (int i = ; i < size; i++)
Insert(arr[i],root);
}
// 析構函數
~BST()
{
makeEmpty(_pRoot);
}
// 插入函數
bool Insert(const T n)
{
return Insert(n, _pRoot);
}
// 搜尋函數
bool Search(const T n)
{
return Search(n, _pRoot);
}
// 删除函數
bool Remove(const T n)
{
return Remove(n, _pRoot);
}
// 顯示二叉樹
void printTree()const
{
printTree(_pRoot);
}
private:
BSTNode<T> * _pRoot; // 二叉樹根指針
// 置空函數
void makeEmpty(BSTNode<T> * ptr)
{
if (ptr == NULL)
return;
makeEmpty(ptr->_pLeft);
makeEmpty(ptr->_pRight);
delete ptr;
}
// 插入函數
bool Insert(const T n, BSTNode<T> *& ptr)
{
if (ptr == NULL)
{
ptr = new BSTNode<T>(n);
if (ptr == NULL)
cout << "記憶體配置設定錯誤!" << endl;
return false;
}
else if (n < ptr->_data)
Insert(n, ptr->_pLeft);
else if (n > ptr->_data)
Insert(n, ptr->_pRight);
else
{
cout << "資料已存在!" << endl;
return false;
}
return true;
}
// 搜尋函數
bool Search(const T n, BSTNode<T> * ptr)
{
while (ptr)
{
if (ptr->_data == n)
return true;
else if (ptr->_data < n)
ptr = ptr->_pRight;
else
ptr = ptr->_pLeft;
}
cout << "内容不存在!" << endl;
return false;
}
// 删除函數
bool Remove(const T n, BSTNode<T> *& ptr)
{
BSTNode<T> * del; // 删除的結點
if (ptr == NULL)
{
cout << "資料為空!" << endl;
return false;
}
if (ptr->_data == n)
{
// 左右子女均存在的情況
if (ptr->_pLeft != NULL && ptr->_pRight != NULL)
{
del = ptr->_pRight;
while (del->_pLeft != NULL)
del = del->_pLeft;
ptr->_data = del->_data;
Remove(del->_data, ptr->_pRight);
}
else
{
del = ptr;
/*if (ptr->_pLeft != NULL)
ptr = ptr->_pLeft;
else if (ptr->_pRight != NULL)
ptr = ptr->_pRight;
else
ptr = NULL;*/
if (ptr->_pRight != NULL)
ptr = ptr->_pRight;
else
ptr = ptr->_pLeft;
delete del;
return true;
}
}
else if (ptr->_data > n)
Remove(n, ptr->_pLeft);
else if (ptr->_data < n)
Remove(n, ptr->_pRight);
}
// 顯示輸出函數
bool printTree(BSTNode<T> * ptr)const
{
if (ptr == NULL)
return false;
printTree(ptr->_pLeft);
cout << ptr->_data << " ";
printTree(ptr->_pRight);
}
};
int main()
{
BST<int> s;
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Insert();
s.Remove();
s.printTree();
return ;
}