拓扑排序（Topological Sorting）

拓扑排序（Topological Sorting）

这篇文章我们来讲一下拓扑排序，这可是一个很重要也很实用的算法，面试中常考，工作中常用，无论是互联网公司还是金融公司，考算法的时候都贼喜欢问这个。

拓扑排序其实并不是一个传统意义上的排序算法，它是针对AOV网线性输出的过程，所以我们先来了解一下AOV网是什么东西。

AOV网

拓扑排序算法只适用于AOV网，它是一种有向无环图，那么到底什么是AOV网呢？

在日常生活中，一项大工程可以看作是由若干个小工程组成的，但这些小工程之间必定存在一些先后顺序，也就是说，有些工程必须在其它一些工程完成之后才能开始。我们可以用有向图来形象地表示这些工程之间的先后关系，小工程为顶点，之间的先后关系为有向边，绘制成的有向图就是AOV网。一个AOV网必定是一个有向无环图，也就是不应该带有回路，否则就会出现先后关系的自相矛盾。

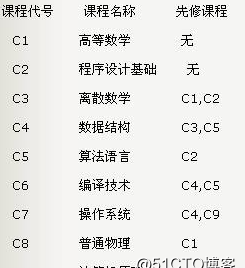
例如，假定一个计算机专业的学生必须完成下图所列出的全部课程。

在这里，每个课程就代表一个小工程，学习一门课程就表示进行一项工程，学习每门课程的先决条件是学完它的全部先修课程。如学习《高等数学》课程则可以随时安排，因为它是基础课程，没有先修课。学习《数据结构》课程就必须安排在学完它的两门先修课程《离散数学》和《算法语言》之后。

若用AOV网来表示这种课程安排的先后关系，则如上图所示。图中的每个顶点代表一门课程，每条有向边代表起点对应的课程是终点对应课程的先修课。从图中可以清楚地看出各课程之间的先修和后续的关系。如课程C5的先修课为C2，后续课程为C4和C6。

拓扑排序

那么拓扑排序到底是干什么的呢？如果我们要安排课表，那么不可能直接把AOV图给学生看，而是需要把它排成一个序列，使得每个课程的先修课都排在该课程的前面，这个过程就称为“拓扑排序”。拓扑排序得到的序列并不是唯一的，就好像你早上穿衣服可以先穿内衣再穿外套，然后再穿裤子，也可以先穿裤子再穿内衣，最后再穿外套，只要内衣在外套之前穿就行。

拓扑排序得到的序列可以帮助我们合理安排一个工程的进度，所以，由AOV网构造拓扑序列具有很高的实际应用价值。

算法思想

构造拓扑序列的拓扑排序算法思想很简单：

（1）选择一个入度为0的顶点；

（2）从AOV网中删除此顶点及以此顶点为起点的关联边；

（3）重复上述两步直到不存在入度为0的顶点为止；

（4）若AOV网中还有顶点，则说明有向图存在回路。

算法实现

class Graph {
	int V;				// 顶点个数 
	int* indegree;		// 顶点入度 
	list<int> *adj;		// 邻接表 
	
	public:
	Graph(int v) {
		this->V = v;
		this->adj = new list<int>[v];
		this->indegree = new int[v];
		for(int i = 0; i < v; i++) {
			this->indegree[i] = 0;
		}
	}
	~Graph() {
		delete [] this->adj;
		delete [] this->indegree;
	}
	void addEdge(int v, int w) {
		this->adj[v].push_back(w);
		this->indegree[w]++;
	}
	vector<int> topologicalSort() {
		vector<int> res;	// 拓扑序列 
		queue<int> que;		// 入度为0顶点集合 
		
		for(int i = 0; i < this->V; i++) {
			if (this->indegree[i] == 0) {
				que.push(i);
			}
		}
		while(!que.empty()) {
			int front = que.front();
			que.pop();
			res.push_back(front);
			for(int item:this->adj[front]) {
				if (!(--this->indegree[item])) {
					que.push(item);
				}
			}
		}
		return res.size() == this->V ? res : vector<int> ();
	}
};
      

测试

int main(){
    Graph graph(8);
    graph.addEdge(0,1);
    graph.addEdge(0,2);
    graph.addEdge(2,4);
    graph.addEdge(1,4);
    graph.addEdge(1,3);
    graph.addEdge(4,3);
    graph.addEdge(4,5);
    graph.addEdge(4,6);
    graph.addEdge(3,5);
    graph.addEdge(6,7);
    graph.addEdge(5,7);
    graph.addEdge(3,7);
    for (int item:graph.topologicalSort()) {
    	cout << item << " ";
	}
    return 0;
}
      

练习题