拓撲排序（Topological Sorting）

拓撲排序（Topological Sorting）

這篇文章我們來講一下拓撲排序，這可是一個很重要也很實用的算法，面試中常考，工作中常用，無論是網際網路公司還是金融公司，考算法的時候都賊喜歡問這個。

拓撲排序其實并不是一個傳統意義上的排序算法，它是針對AOV網線性輸出的過程，是以我們先來了解一下AOV網是什麼東西。

AOV網

拓撲排序算法隻适用于AOV網，它是一種有向無環圖，那麼到底什麼是AOV網呢？

在日常生活中，一項大工程可以看作是由若幹個小工程組成的，但這些小工程之間必定存在一些先後順序，也就是說，有些工程必須在其它一些工程完成之後才能開始。我們可以用有向圖來形象地表示這些工程之間的先後關系，小工程為頂點，之間的先後關系為有向邊，繪制成的有向圖就是AOV網。一個AOV網必定是一個有向無環圖，也就是不應該帶有回路，否則就會出現先後關系的自相沖突。

例如，假定一個計算機專業的學生必須完成下圖所列出的全部課程。

在這裡，每個課程就代表一個小工程，學習一門課程就表示進行一項工程，學習每門課程的先決條件是學完它的全部先修課程。如學習《高等數學》課程則可以随時安排，因為它是基礎課程，沒有先修課。學習《資料結構》課程就必須安排在學完它的兩門先修課程《離散數學》和《算法語言》之後。

若用AOV網來表示這種課程安排的先後關系，則如上圖所示。圖中的每個頂點代表一門課程，每條有向邊代表起點對應的課程是終點對應課程的先修課。從圖中可以清楚地看出各課程之間的先修和後續的關系。如課程C5的先修課為C2，後續課程為C4和C6。

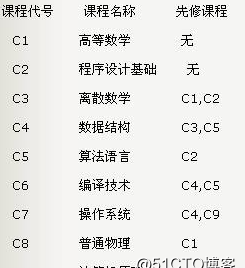
拓撲排序

那麼拓撲排序到底是幹什麼的呢？如果我們要安排課表，那麼不可能直接把AOV圖給學生看，而是需要把它排成一個序列，使得每個課程的先修課都排在該課程的前面，這個過程就稱為“拓撲排序”。拓撲排序得到的序列并不是唯一的，就好像你早上穿衣服可以先穿内衣再穿外套，然後再穿褲子，也可以先穿褲子再穿内衣，最後再穿外套，隻要内衣在外套之前穿就行。

拓撲排序得到的序列可以幫助我們合理安排一個工程的進度，是以，由AOV網構造拓撲序列具有很高的實際應用價值。

算法思想

構造拓撲序列的拓撲排序算法思想很簡單：

（1）選擇一個入度為0的頂點；

（2）從AOV網中删除此頂點及以此頂點為起點的關聯邊；

（3）重複上述兩步直到不存在入度為0的頂點為止；

（4）若AOV網中還有頂點，則說明有向圖存在回路。

算法實作

class Graph {
	int V;				// 頂點個數 
	int* indegree;		// 頂點入度 
	list<int> *adj;		// 鄰接表 
	
	public:
	Graph(int v) {
		this->V = v;
		this->adj = new list<int>[v];
		this->indegree = new int[v];
		for(int i = 0; i < v; i++) {
			this->indegree[i] = 0;
		}
	}
	~Graph() {
		delete [] this->adj;
		delete [] this->indegree;
	}
	void addEdge(int v, int w) {
		this->adj[v].push_back(w);
		this->indegree[w]++;
	}
	vector<int> topologicalSort() {
		vector<int> res;	// 拓撲序列 
		queue<int> que;		// 入度為0頂點集合 
		
		for(int i = 0; i < this->V; i++) {
			if (this->indegree[i] == 0) {
				que.push(i);
			}
		}
		while(!que.empty()) {
			int front = que.front();
			que.pop();
			res.push_back(front);
			for(int item:this->adj[front]) {
				if (!(--this->indegree[item])) {
					que.push(item);
				}
			}
		}
		return res.size() == this->V ? res : vector<int> ();
	}
};
      

測試

int main(){
    Graph graph(8);
    graph.addEdge(0,1);
    graph.addEdge(0,2);
    graph.addEdge(2,4);
    graph.addEdge(1,4);
    graph.addEdge(1,3);
    graph.addEdge(4,3);
    graph.addEdge(4,5);
    graph.addEdge(4,6);
    graph.addEdge(3,5);
    graph.addEdge(6,7);
    graph.addEdge(5,7);
    graph.addEdge(3,7);
    for (int item:graph.topologicalSort()) {
    	cout << item << " ";
	}
    return 0;
}
      

練習題