 |
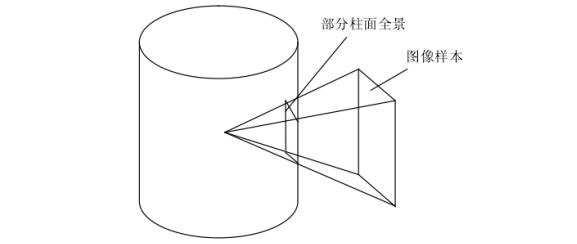
柱面全景是最为简单的全景虚拟。所谓柱面全景,可以理解为以节点为中心的具有一定高度的圆柱形的平面,平面外部的景物投影在这个平面上。如图所示。
用户可以在全景图像中 360 度的范围内任意切换视线,也可以在一个视线上改变视角,来取得接近或远离的效果,也可以认为是球面全景图的一种简化。用户在水平方向上有 360度的视角,在垂直方向上也可以做一定的视角变化,但是角度范围则受到限制。由于柱面模型的图像质量均匀,细节真实程度更高,应用范围比较广泛。
柱面全景图像也较为容易处理,因为可以将圆柱面沿轴向切开并展开在一个平面上,传统的图像处理方法常常可以直接使用。柱面全景图像并不要求照相机的标定十分准确。所以将柱面全景图显著优点归纳为以下两点:
1)它的单幅照片的获取方式比立方体形式和球面形式的获取方式简单。所需的设备只有普通的相机和一个允许连续“转动”的三角架。
2)柱面全景图容易展开为一个矩形图像,可直接用计算机常用的图像格式进行存储和访问。虽然柱面形式的全景图在垂直方向允许参与者视线的转动角度小于 180 度,但是在绝大多数应用中,水平方向的 360 度环视场景已足以表达空间信息。
// ConsoleApplication.cpp : 定义控制台应用程序的入口点。
//
#
include
"stdafx.h"
using
namespace
std;
using
namespace
cv;
#
define
PI 3.14159
int
_tmain(
int
argc, _TCHAR* argv[])
{
Mat src = imread("e:/template/Univ4.jpg");
Mat result = src.clone();
for
(
int
i=0;i<result.rows;i++)
{
for
(
int
j=0;j<result.cols;j++)
result.at<Vec3b>(i,j)=0;
}
int
W = src.cols;
int
H = src.rows;
float
r = W/(2*tan(PI/6));
float
k = 0;
float
fx=0;
float
fy=0;
for
(
int
i=0;i<src.rows;i++)
{
for
(
int
j=0;j<src.cols;j++)
{
k = sqrt((
float
)(r*r+(W/2-j)*(W/2-j)));
fx = r*sin(PI/6)+r*sin(atan((j -W/2 )/r));
fy = H/2 +r*(i-H/2)/k;
int
ix = (
int
)fx;
int
iy = (
int
)fy;
if
(ix<W&&ix>=0&&iy<H&&iy>=0)
result.at<Vec3b>(iy,ix)= src.at<Vec3b>(i,j);
}
}
imshow("src",src);
imshow("result",result);
waitKey();
return
0;
}
目前方向:图像拼接融合、图像识别
联系方式:[email protected]