0 前言
网络已经成为我们传递信息的主要平台, 为我们提供诸多便捷的同时, 也存在一些安全问题, 特别是一些重要信息的传递.如果在信息传递前先对其进行加密, 能够在一定程度上保护所传递的信息.数字图像作为重要的信息资源在人们的生活中发挥着越来越重要的作用[1], 因此, 数字图像的加密是一项值得研究的重要课题.本文介绍的就是一种基于Arnold变换的图像加解密算法。
1 Arnold变换
将N*N图像上的点 (x, y) 通过如下变换转成 (x′, y′) 如式 (1) , 该变换即称为Arnold变换.通过变换公式可发现, 其变换的本质是点的位置的变换, 并且这种变换保证变换前后的点保持一一对应的关系。
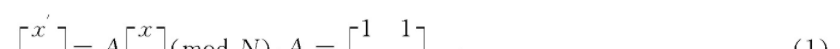
如果将一次变换的输出作为下一次变换的输入, 这就是迭代变换如式 (2) .当一次变换置乱效果不佳时, 往往需要迭代变换获得更好的置乱效果。
2 基于Arnold变换的图像加解密
图像加密也称图像置乱, 是对图像的像素进行混乱和扩散, 使加密后的图像在视觉上无法获得有效信息.空域加密是常用的方法, 分为空域置乱和序列加密.空域置乱是对像素坐标进行变换使其混乱, 解密时恢复原像素坐标.图像的加密既可以作为独立的信息隐藏方法, 也可以用来作为数字水印技术中图像水印的预处理。
加密图像可以是灰度图像也可以是彩色图像, 如果是灰度图像则需要将各点的灰度值带到新的坐标点, 如果是彩色图像则需要将各点的RGB值带到新的坐标点.本文所加密的图像为彩色图像, 因此首先保存原图点 (x, y) 处的RGB值, 然后使用Arnold变换改变点 (x, y) 位置到 (x′, y′) , 同时将原图点 (x, y) 处的RGB值带到 (x′, y′) 处.我们采用256*256的彩色图像作为原始图像如图1a所示, 在Visual Studio2008平台下运用式 (1) 对原图进行一次Arnold变换, 变换后的效果如图1b所示.
由图1可知, 对图像进行一次Arnold变换后仍会留下较多信息, 故在此基础上继续使用Arnold变换, 通过5次变换后 (见图2b) 其结果在视觉上就很难再获得什么有价值的信息, 在视觉上起到了图像加密的作用.同时变换的次数往往可以作为密钥, 从而在一定程度上提高安全性。
图1 原图和一次Arnold变换结果
图2 第2次和第5次Arnold变换结果
然而此时的加密并不完全可靠, 若已知采用Arnold变换作为加密方式, 则通过暴力求解法, 经过若干次的变换还是可以解密出原图.因此在一般情况下, 我们往往需要在Arnold变换中加入密钥 (ku, kv) , 以提高安全性, 其公式如下:
当需要对图像进行解密时, 则根据加密后的图像中的像素点与原图中的像素点是一一对应的关系进行解密, 因此图像解密的过程为:根据原图中像素点的坐标 (x, y) 按照Arnold变换算出新图中像素点的坐标 (x′, y′) , 获取新像素点 (x′, y′) 的RGB值, 将该值归还给 (x, y) .根据加密过程使用的变换次数, 解密时则要将以上过程重复相应的次数就可以恢复原图 (见图3) 。
3 基于三维Arnold变换的图像加密
前面提到的图像置乱是通过打乱像素点位置而达成目标, 图像的颜色分量值是保持不变的.因此为了提高加密效果, 我们可以在像素点位置已乱的前提下, 再通过改变RGB颜色分量的值对图像进行加密.采用如下三维Arnold变换 (如式4) 进行RGB分量值的改变。
我们将一次Arnold变换后的图像作为原始图像, 在此基础上对各像素点的RGB采用以上公式进行扰乱, 获得如图4所示结果.通过两种加密方式的综合, 则进一步提高了加密图像的安全性.式4中的值可以做相应的改变, 同时可以将变换的次数作为密钥提高安全性。
图3 第五次Arnold变换结果, 恢复后的加密图像
图4 第一次Arnold变换结果, RGB扰乱后的加密图像
1 matlab版本
2014a
2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社,2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社,2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社,2015.