0 前言
網絡已經成為我們傳遞資訊的主要平台, 為我們提供諸多便捷的同時, 也存在一些安全問題, 特别是一些重要資訊的傳遞.如果在資訊傳遞前先對其進行加密, 能夠在一定程度上保護所傳遞的資訊.數字圖像作為重要的資訊資源在人們的生活中發揮着越來越重要的作用[1], 是以, 數字圖像的加密是一項值得研究的重要課題.本文介紹的就是一種基于Arnold變換的圖像加解密算法。
1 Arnold變換
将N*N圖像上的點 (x, y) 通過如下變換轉成 (x′, y′) 如式 (1) , 該變換即稱為Arnold變換.通過變換公式可發現, 其變換的本質是點的位置的變換, 并且這種變換保證變換前後的點保持一一對應的關系。
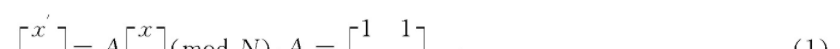
如果将一次變換的輸出作為下一次變換的輸入, 這就是疊代變換如式 (2) .當一次變換置亂效果不佳時, 往往需要疊代變換獲得更好的置亂效果。
2 基于Arnold變換的圖像加解密
圖像加密也稱圖像置亂, 是對圖像的像素進行混亂和擴散, 使加密後的圖像在視覺上無法獲得有效資訊.空域加密是常用的方法, 分為空域置亂和序列加密.空域置亂是對像素坐标進行變換使其混亂, 解密時恢複原像素坐标.圖像的加密既可以作為獨立的資訊隐藏方法, 也可以用來作為數字水印技術中圖像水印的預處理。
加密圖像可以是灰階圖像也可以是彩色圖像, 如果是灰階圖像則需要将各點的灰階值帶到新的坐标點, 如果是彩色圖像則需要将各點的RGB值帶到新的坐标點.本文所加密的圖像為彩色圖像, 是以首先儲存原圖點 (x, y) 處的RGB值, 然後使用Arnold變換改變點 (x, y) 位置到 (x′, y′) , 同時将原圖點 (x, y) 處的RGB值帶到 (x′, y′) 處.我們采用256*256的彩色圖像作為原始圖像如圖1a所示, 在Visual Studio2008平台下運用式 (1) 對原圖進行一次Arnold變換, 變換後的效果如圖1b所示.
由圖1可知, 對圖像進行一次Arnold變換後仍會留下較多資訊, 故在此基礎上繼續使用Arnold變換, 通過5次變換後 (見圖2b) 其結果在視覺上就很難再獲得什麼有價值的資訊, 在視覺上起到了圖像加密的作用.同時變換的次數往往可以作為密鑰, 進而在一定程度上提高安全性。
圖1 原圖和一次Arnold變換結果
圖2 第2次和第5次Arnold變換結果
然而此時的加密并不完全可靠, 若已知采用Arnold變換作為加密方式, 則通過暴力求解法, 經過若幹次的變換還是可以解密出原圖.是以在一般情況下, 我們往往需要在Arnold變換中加入密鑰 (ku, kv) , 以提高安全性, 其公式如下:
當需要對圖像進行解密時, 則根據加密後的圖像中的像素點與原圖中的像素點是一一對應的關系進行解密, 是以圖像解密的過程為:根據原圖中像素點的坐标 (x, y) 按照Arnold變換算出新圖中像素點的坐标 (x′, y′) , 擷取新像素點 (x′, y′) 的RGB值, 将該值歸還給 (x, y) .根據加密過程使用的變換次數, 解密時則要将以上過程重複相應的次數就可以恢複原圖 (見圖3) 。
3 基于三維Arnold變換的圖像加密
前面提到的圖像置亂是通過打亂像素點位置而達成目标, 圖像的顔色分量值是保持不變的.是以為了提高加密效果, 我們可以在像素點位置已亂的前提下, 再通過改變RGB顔色分量的值對圖像進行加密.采用如下三維Arnold變換 (如式4) 進行RGB分量值的改變。
我們将一次Arnold變換後的圖像作為原始圖像, 在此基礎上對各像素點的RGB采用以上公式進行擾亂, 獲得如圖4所示結果.通過兩種加密方式的綜合, 則進一步提高了加密圖像的安全性.式4中的值可以做相應的改變, 同時可以将變換的次數作為密鑰提高安全性。
圖3 第五次Arnold變換結果, 恢複後的加密圖像
圖4 第一次Arnold變換結果, RGB擾亂後的加密圖像
1 matlab版本
2014a
2 參考文獻
[1] 蔡利梅.MATLAB圖像處理——理論、算法與執行個體分析[M].清華大學出版社,2020.
[2]楊丹,趙海濱,龍哲.MATLAB圖像處理執行個體詳解[M].清華大學出版社,2013.
[3]周品.MATLAB圖像處理與圖形使用者界面設計[M].清華大學出版社,2013.
[4]劉成龍.精通MATLAB圖像處理[M].清華大學出版社,2015.