数组是一种非常基础的数据结构,很多人都会觉得数组非常简单,在我们使用的编程语言当中几乎都有数组这种数据结构,我们平常使用的也非常广泛。虽然如此,但是我们真的完全了解数组吗?比如数组为什么可以支持随机访问,数组具体有哪些特性,我们如何高效的实现在数组中插入或者删除一个元素,这些问题大家是否都能不假思索的回答呢?
数组是指的是用一组连续的内存空间,来存储一组具有相同类型的数据的线性表数据结构。
这个定义里面有数组的两个非常重要的特性:
连续的内存空间和相同的数据类型
连续的内存空间就是说数组中所有的元素都必须连续排列在一起,中间不允许有空位置。正是数组的这个特性决定了数组支持随机访问,因为我们可以通过数组占用内存的起始内存地址,再根据每个元素占用空间就可以计算出任意位置元素的内存地址,进而直接访问它。然而数组的这个特性也带来了不利的一面,那就是删除一个元素时,为了确保数组空间的连续性,这个元素之后的所有元素都必须往前移,这也就导致了删除元素的最坏时间复杂度为 <code>O(n)</code>。插入元素也是同理,所以数组具有高效的访问操作的同时却具有低效的插入和删除操作。
数据连续的内存空间也决定了数组无法直接进行扩容,当我们需要对数组进行扩容时,必须重新再申请一块连续的内存空间,然后将旧数组的所有元素赋值到新数组当中,可以想象,这种方式肯定是消耗性能的。
<code>Java</code> 中的 <code>ArrayList</code> 集合类,底层就是使用数组实现的,虽然我们不需要手动进行扩容,但是一旦超过了定义的存储范围,触发扩容操作时,<code>ArrayList</code> 底层就是通过 <code>Arrays.copyOf</code> 的方式进行的扩容:
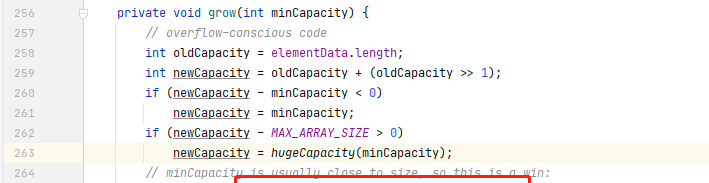
而<code>Arrays.copyOf</code> 方法就会申请一个新数组来存储旧数组的元素。正是因为数组的这种扩容方式会带来性能上的消耗,所以当我们使用 <code>ArrayList</code> 时,如果可以预判长度,最好指定一个长度(<code>HashMap</code> 也是同理),这样可以避免后期触发扩容。
线性表结构
线性表结构的意思就是数据和线一样排列成一排,也就是说只有一条线可以往后(往前)走,没有其他分叉路,其他的比如链表,栈,队列等都属于线性结构,而二叉树,图,堆等数据结构就属于非线性表结构。
几乎所有的语言中都提供了数组的数据类型,在这里以 <code>Java</code> 语言为例。
在 <code>Java</code> 中可以通过以下方式定义一个数组:
方式一(<code>[]</code> 放前放后都可以):直接定义长度,然后赋值时如果值都是有规律的话可以通过循环赋值。
方式二:直接定义数组元素。
方式三:直接定义数组元素,在算法中一般都是这种写法,这种方式也可以看做是方式二的简写形式。
单调数组指的就是一个数组是有序的,也就是说数组中的元素要么是递增的,要么就是递减的。
单调递增数组:对于所有 <code>i <= j</code>,有 <code>A[i] <= A[j]</code>。
单调递减数组:对于所有 <code>i <= j</code>,有 <code>A[i] >= A[j]</code>。
在算法当中,如果给的数组是一个单调数组,那么我们首先应该想到的是二分查找法,关于二分查找在算法系列的后续文章会专门讲解,本文不会展开。
在数组当中,我们需要注意区分数组的长度(length)和数组的有效位数(size)。
比如下面这个数组:
在这个数组当中,我们定义了数组的长度是 <code>5</code>,但是里面只有一个元素,这时候我们就需要再定义一个 <code>size</code>,用来标记当前数组有效位数。
我们看下面两行代码:
我们都知道,<code>ArrayList</code> 的底层是数组,当我们初始化一个 <code>ArrayList</code> 的时候,底层会创建一个 <code>16</code> 位长度的数组。
但是我们这里只添加了一个元素,所以 <code>size</code> 就是 <code>1</code>,<code>ArrayList</code> 中维护了一个 <code>size</code> 属性来记录数组中的有效元素,当我们每次添加元素的时候,<code>size</code> 才会增加。
所以本文后面的例子中也一样,我们需要时刻记得维护 <code>size</code>,否则就会输出无效数据位或者有效数据无法被输出。
数组本身并不难,但是很多高级算法都会依托数组,所以数组是基础的基础,对于数组的增删改查操作我们需要非常熟练,在操作数组时,我们尤其要注意的就是数组越界的问题,在 <code>Java</code> 这种本身就提供了安全机制的情况下,越界会直接抛出异常,但是对于 <code>C</code> 语言这种,数组越界就会访问到其他内存地址,造成一些未知的错误产生。
在数组中,如果给定一个下标,我们可以直接通过下标访问元素,如果给定的是一个元素的值,那么我们就需要找到下标,而寻找指定元素的下标我们就可以通过遍历的方式查找(当然如果是单调数组我们可以通过二分查找法来提高效率)。
如下就是一个根据给定元素的值来查找元素下标的示例:
在数组中删除一个元素时,为了保证数组内存的连续性,后面的所有元素都必须往前移动。当我们删除的元素正好是数组尾部,那么时间复杂度就是 <code>O(1)</code>,如果删除的元素位于头部,那么时间复杂度就是 <code>O(n)</code>。
下面就是一个删除数组中元素的例子:
这道题目本身很简单,但是这个示例当中也有两个关键点:
数组的边界控制
size 的维护
上面示例中元素是直接给出了下标,如果给的是元素的值呢?那么这时候我们就需要先找到当前元素在数组中的下标,然后再根据下标进行删除。
假如给定的数组中还有空位,那么要在数组中新增一个元素很简单,直接放到 <code>arr[size]</code> 的位置就行,比如下面的例子,因为数组只是初始化了一个空间,没有任何元素,所以添加的时候只需要使用简单的 <code>arr[index]</code> 进行赋值就可以:
现在假如给定的是一个单调递增数组,我们要往里面插入一个元素,这时候就没那么简单了,因为我们需要保证数组的顺序,所以不能直接插入到最后,必须得先确定插入的位置,这时候我们有两种办法:
方法一:根据元素找到需要插入的位置,然后执行插入操作,插入的同时,其他元素都往后移动。
方法二:直接从后往前开始比较,如果比较的结果比插入元素大,那么往后移动一位,直到找到自己的插入位置。
下面的示例就是利用方法二,从后往前开始遍历查找并插入元素:
所以其实可以看到,插入一个元素的最坏时间复杂度也是 <code>O(n)</code>,那么有没有办法使得插入元素的时间复杂度达到 <code>O(1)</code> 呢?
在特定场景下往数组中插入一个元素时间复杂度是可以达到 <code>O(1)</code> 的。
比如我们的数组是无序的,插入一个元素也不在乎顺序,也没有指定插入元素的位置,那么这时候就可以选择直接插入尾部;如果插入元素时指定了一个插入位置,如果不关心顺序的话也可以采用一种巧妙的办法来实现:
这里其实就是直接将需要插入元素的位置上的原有元素放到最后,然后再直接插入,避免了数组的移动,实现了 <code>O(1)</code> 时间复杂度的插入。
修改元素如果不关心顺序那么直接覆盖即可,如果关心顺序,那么就需要结合上面的方法,先找到需要插入的位置,然后将原有数据删除,再插入新数据。
在数组相关的算法题中,双指针思想是最核心最重要的一个思想。我们知道,操作数组可能会带来大量数组元素的移动,避免元素的移动直接就可以提升一个算法的效率,而双指针的用法恰恰就可以减少数组元素的移动。
指针是什么?所谓的指针其实就是一个指向了具体内存地址的引用,或者说我们根据这个指针可以直接访问到内存地址。我们平常遍历数组的时候,会有一个下标,那么这个下标就可以算是一个指针,因为通过这个下标,我们可以直接访问素组元素。所以在数组中,所谓的双指针,其实就是指的两个下标。
下面我们就以 <code>leetcode</code> 上的第 <code>26</code> 题为例子来具体看看双指针的妙用。
题目的描述是这样的:给你一个有序数组 <code>nums</code>,请你原地删除重复出现的元素,使每个元素只出现一次 ,返回删除后数组的新长度。注意不要使用额外的数组空间,你必须在原地修改输入数组并在使用 <code>O(1)</code> 额外空间的条件下完成。
这道题最直接的第一反应应该有两个思路:
方法一:定义新数组来存储,空间复杂度为 <code>O(n)</code>
新建一个新数组,然后从头开始遍历 <code>nums</code>,因为数组是有序的,所以相同的元素一定是连续的,我们先把第一个元素放到新数组,然后开始遍历,发现 <code>nums</code> 中元素和新数组第一个元素相同就跳过,发现不同就存入新数组,然后再继续遍历 <code>nums</code> 并和新数组的第二个元素比较,依次类推。
方法二:双重循环遍历法
双重循环遍历数组,发现相同的数据则删除,删除的同时把后面的元素都往前移动。
这两种写法在这里就不写示例,实现起来相对比较简单,正常都能想到。但是方法一空间复杂度不符合题目要求,方法二虽然实现了,但是会带来大量的数组移动,而且还比较容易出错。
这道题如果利用双指针来实现,就会非常简洁,高效。
这道题我们可以定义两个指针: ⼀个指向有效数组的最后⼀个位置(validIndex),⼀个指针负责数组遍历(index),当两个指针指向的值不⼀样时,将 <code>validIndex</code> 向后移动,并将 <code>index</code> 对应的值赋给 <code>validIndex</code>,如此当 <code>index</code> 遍历完数组之后,<code>validIndex</code> 就是有效数组的最后一个下标。
下面我们通过一个具体的例子来分析一下双指针的执行过程。
假设我们有一个数组 <code>int[] arr = {1,1,2,3}</code>,这时候我们定义两个指针 <code>validIndex</code> 和 <code>index</code>,初始都指向元素 <code>1</code>,也就是下标 <code>0</code>:
这时候开始遍历,两个值比较,发现相等,<code>validIndex</code> 不移动,<code>index</code> 往后移动到第二个元素 <code>1</code> 所在的位置:
这时候继续比较,发现还是相等,<code>validIndex</code> 继续保持原来位置不动,<code>index</code> 则继续往后移动到 <code>2</code> 的位置:
这时候比较,发现 <code>1</code> 和 <code>2</code> 已经不相等了,这时候需要把 <code>validIndex</code> 往后移动到第二个位置,同时把第三个位置的元素 <code>2</code> 赋值给新 <code>validIndex</code>,并且 <code>index</code> 自己也继续往后移动到 <code>3</code> 的位置。
继续比较,发现 <code>2</code> 和 <code>3</code> 也不想等,继续把 <code>validIndex</code> 往后移动,同时把 <code>3</code> 赋值给新 <code>validIndex</code>,此时因为 <code>index</code> 已经到达数组末尾,循环结束。
这时候得到的 <code>validIndex</code> 就是不重复数组元素的下标,用这种方式避免了数组的大量移动,仅仅通过覆盖的方式就达到了目的,下面就是双指针的代码实现(示例中代码 <code>validLength</code> 初始为 <code>1</code>,所以比较的需要时候是 <code>arr[validLength - 1]</code>)需要减 <code>1</code>,而赋值的时候是 <code>arr[validLength++]</code>,不需要加 <code>1</code>:
本文主要讲述了数据结构中最基础的一种数据结构数组的特性,并且分析了数组的特性决定了数组的访问是高效的,但是插入和删除是低效的原因。数组本身比较简单,但是数组又是许多高级算法的载体,所以我们如果想要学习高级算法,那么数组的增删改查是必须要掌握的,同时最后我们通过一个例子介绍了双指针思想的利用,在数组中的相关操作中,利用双指针可以巧妙的避免操作数组时带来的大量元素移动。