數組是一種非常基礎的資料結構,很多人都會覺得數組非常簡單,在我們使用的程式設計語言當中幾乎都有數組這種資料結構,我們平常使用的也非常廣泛。雖然如此,但是我們真的完全了解數組嗎?比如數組為什麼可以支援随機通路,數組具體有哪些特性,我們如何高效的實作在數組中插入或者删除一個元素,這些問題大家是否都能不假思索的回答呢?
數組是指的是用一組連續的記憶體空間,來存儲一組具有相同類型的資料的線性表資料結構。
這個定義裡面有數組的兩個非常重要的特性:
連續的記憶體空間和相同的資料類型
連續的記憶體空間就是說數組中所有的元素都必須連續排列在一起,中間不允許有空位置。正是數組的這個特性決定了數組支援随機通路,因為我們可以通過數組占用記憶體的起始記憶體位址,再根據每個元素占用空間就可以計算出任意位置元素的記憶體位址,進而直接通路它。然而數組的這個特性也帶來了不利的一面,那就是删除一個元素時,為了確定數組空間的連續性,這個元素之後的所有元素都必須往前移,這也就導緻了删除元素的最壞時間複雜度為 <code>O(n)</code>。插入元素也是同理,是以數組具有高效的通路操作的同時卻具有低效的插入和删除操作。
資料連續的記憶體空間也決定了數組無法直接進行擴容,當我們需要對數組進行擴容時,必須重新再申請一塊連續的記憶體空間,然後将舊數組的所有元素指派到新數組當中,可以想象,這種方式肯定是消耗性能的。
<code>Java</code> 中的 <code>ArrayList</code> 集合類,底層就是使用數組實作的,雖然我們不需要手動進行擴容,但是一旦超過了定義的存儲範圍,觸發擴容操作時,<code>ArrayList</code> 底層就是通過 <code>Arrays.copyOf</code> 的方式進行的擴容:
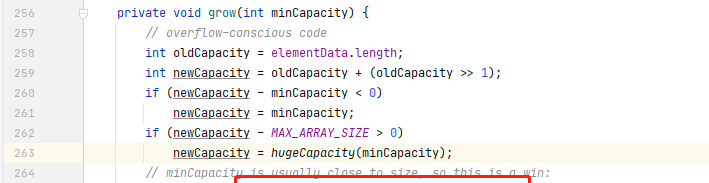
而<code>Arrays.copyOf</code> 方法就會申請一個新數組來存儲舊數組的元素。正是因為數組的這種擴容方式會帶來性能上的消耗,是以當我們使用 <code>ArrayList</code> 時,如果可以預判長度,最好指定一個長度(<code>HashMap</code> 也是同理),這樣可以避免後期觸發擴容。
線性表結構
線性表結構的意思就是資料和線一樣排列成一排,也就是說隻有一條線可以往後(往前)走,沒有其他分叉路,其他的比如連結清單,棧,隊列等都屬于線性結構,而二叉樹,圖,堆等資料結構就屬于非線性表結構。
幾乎所有的語言中都提供了數組的資料類型,在這裡以 <code>Java</code> 語言為例。
在 <code>Java</code> 中可以通過以下方式定義一個數組:
方式一(<code>[]</code> 放前放後都可以):直接定義長度,然後指派時如果值都是有規律的話可以通過循環指派。
方式二:直接定義數組元素。
方式三:直接定義數組元素,在算法中一般都是這種寫法,這種方式也可以看做是方式二的簡寫形式。
單調數組指的就是一個數組是有序的,也就是說數組中的元素要麼是遞增的,要麼就是遞減的。
單調遞增數組:對于所有 <code>i <= j</code>,有 <code>A[i] <= A[j]</code>。
單調遞減數組:對于所有 <code>i <= j</code>,有 <code>A[i] >= A[j]</code>。
在算法當中,如果給的數組是一個單調數組,那麼我們首先應該想到的是二分查找法,關于二分查找在算法系列的後續文章會專門講解,本文不會展開。
在數組當中,我們需要注意區分數組的長度(length)和數組的有效位數(size)。
比如下面這個數組:
在這個數組當中,我們定義了數組的長度是 <code>5</code>,但是裡面隻有一個元素,這時候我們就需要再定義一個 <code>size</code>,用來标記目前數組有效位數。
我們看下面兩行代碼:
我們都知道,<code>ArrayList</code> 的底層是數組,當我們初始化一個 <code>ArrayList</code> 的時候,底層會建立一個 <code>16</code> 位長度的數組。
但是我們這裡隻添加了一個元素,是以 <code>size</code> 就是 <code>1</code>,<code>ArrayList</code> 中維護了一個 <code>size</code> 屬性來記錄數組中的有效元素,當我們每次添加元素的時候,<code>size</code> 才會增加。
是以本文後面的例子中也一樣,我們需要時刻記得維護 <code>size</code>,否則就會輸出無效資料位或者有效資料無法被輸出。
數組本身并不難,但是很多進階算法都會依托數組,是以數組是基礎的基礎,對于數組的增删改查操作我們需要非常熟練,在操作數組時,我們尤其要注意的就是數組越界的問題,在 <code>Java</code> 這種本身就提供了安全機制的情況下,越界會直接抛出異常,但是對于 <code>C</code> 語言這種,數組越界就會通路到其他記憶體位址,造成一些未知的錯誤産生。
在數組中,如果給定一個下标,我們可以直接通過下标通路元素,如果給定的是一個元素的值,那麼我們就需要找到下标,而尋找指定元素的下标我們就可以通過周遊的方式查找(當然如果是單調數組我們可以通過二分查找法來提高效率)。
如下就是一個根據給定元素的值來查找元素下标的示例:
在數組中删除一個元素時,為了保證數組記憶體的連續性,後面的所有元素都必須往前移動。當我們删除的元素正好是數組尾部,那麼時間複雜度就是 <code>O(1)</code>,如果删除的元素位于頭部,那麼時間複雜度就是 <code>O(n)</code>。
下面就是一個删除數組中元素的例子:
這道題目本身很簡單,但是這個示例當中也有兩個關鍵點:
數組的邊界控制
size 的維護
上面示例中元素是直接給出了下标,如果給的是元素的值呢?那麼這時候我們就需要先找到目前元素在數組中的下标,然後再根據下标進行删除。
假如給定的數組中還有空位,那麼要在數組中新增一個元素很簡單,直接放到 <code>arr[size]</code> 的位置就行,比如下面的例子,因為數組隻是初始化了一個空間,沒有任何元素,是以添加的時候隻需要使用簡單的 <code>arr[index]</code> 進行指派就可以:
現在假如給定的是一個單調遞增數組,我們要往裡面插入一個元素,這時候就沒那麼簡單了,因為我們需要保證數組的順序,是以不能直接插入到最後,必須得先确定插入的位置,這時候我們有兩種辦法:
方法一:根據元素找到需要插入的位置,然後執行插入操作,插入的同時,其他元素都往後移動。
方法二:直接從後往前開始比較,如果比較的結果比插入元素大,那麼往後移動一位,直到找到自己的插入位置。
下面的示例就是利用方法二,從後往前開始周遊查找并插入元素:
是以其實可以看到,插入一個元素的最壞時間複雜度也是 <code>O(n)</code>,那麼有沒有辦法使得插入元素的時間複雜度達到 <code>O(1)</code> 呢?
在特定場景下往數組中插入一個元素時間複雜度是可以達到 <code>O(1)</code> 的。
比如我們的數組是無序的,插入一個元素也不在乎順序,也沒有指定插入元素的位置,那麼這時候就可以選擇直接插入尾部;如果插入元素時指定了一個插入位置,如果不關心順序的話也可以采用一種巧妙的辦法來實作:
這裡其實就是直接将需要插入元素的位置上的原有元素放到最後,然後再直接插入,避免了數組的移動,實作了 <code>O(1)</code> 時間複雜度的插入。
修改元素如果不關心順序那麼直接覆寫即可,如果關心順序,那麼就需要結合上面的方法,先找到需要插入的位置,然後将原有資料删除,再插入新資料。
在數組相關的算法題中,雙指針思想是最核心最重要的一個思想。我們知道,操作數組可能會帶來大量數組元素的移動,避免元素的移動直接就可以提升一個算法的效率,而雙指針的用法恰恰就可以減少數組元素的移動。
指針是什麼?所謂的指針其實就是一個指向了具體記憶體位址的引用,或者說我們根據這個指針可以直接通路到記憶體位址。我們平常周遊數組的時候,會有一個下标,那麼這個下标就可以算是一個指針,因為通過這個下标,我們可以直接通路素組元素。是以在數組中,所謂的雙指針,其實就是指的兩個下标。
下面我們就以 <code>leetcode</code> 上的第 <code>26</code> 題為例子來具體看看雙指針的妙用。
題目的描述是這樣的:給你一個有序數組 <code>nums</code>,請你原地删除重複出現的元素,使每個元素隻出現一次 ,傳回删除後數組的新長度。注意不要使用額外的數組空間,你必須在原地修改輸入數組并在使用 <code>O(1)</code> 額外空間的條件下完成。
這道題最直接的第一反應應該有兩個思路:
方法一:定義新數組來存儲,空間複雜度為 <code>O(n)</code>
建立一個新數組,然後從頭開始周遊 <code>nums</code>,因為數組是有序的,是以相同的元素一定是連續的,我們先把第一個元素放到新數組,然後開始周遊,發現 <code>nums</code> 中元素和新數組第一個元素相同就跳過,發現不同就存入新數組,然後再繼續周遊 <code>nums</code> 并和新數組的第二個元素比較,依次類推。
方法二:雙重循環周遊法
雙重循環周遊數組,發現相同的資料則删除,删除的同時把後面的元素都往前移動。
這兩種寫法在這裡就不寫示例,實作起來相對比較簡單,正常都能想到。但是方法一空間複雜度不符合題目要求,方法二雖然實作了,但是會帶來大量的數組移動,而且還比較容易出錯。
這道題如果利用雙指針來實作,就會非常簡潔,高效。
這道題我們可以定義兩個指針: ⼀個指向有效數組的最後⼀個位置(validIndex),⼀個指針負責數組周遊(index),當兩個指針指向的值不⼀樣時,将 <code>validIndex</code> 向後移動,并将 <code>index</code> 對應的值賦給 <code>validIndex</code>,如此當 <code>index</code> 周遊完數組之後,<code>validIndex</code> 就是有效數組的最後一個下标。
下面我們通過一個具體的例子來分析一下雙指針的執行過程。
假設我們有一個數組 <code>int[] arr = {1,1,2,3}</code>,這時候我們定義兩個指針 <code>validIndex</code> 和 <code>index</code>,初始都指向元素 <code>1</code>,也就是下标 <code>0</code>:
這時候開始周遊,兩個值比較,發現相等,<code>validIndex</code> 不移動,<code>index</code> 往後移動到第二個元素 <code>1</code> 所在的位置:
這時候繼續比較,發現還是相等,<code>validIndex</code> 繼續保持原來位置不動,<code>index</code> 則繼續往後移動到 <code>2</code> 的位置:
這時候比較,發現 <code>1</code> 和 <code>2</code> 已經不相等了,這時候需要把 <code>validIndex</code> 往後移動到第二個位置,同時把第三個位置的元素 <code>2</code> 指派給新 <code>validIndex</code>,并且 <code>index</code> 自己也繼續往後移動到 <code>3</code> 的位置。
繼續比較,發現 <code>2</code> 和 <code>3</code> 也不想等,繼續把 <code>validIndex</code> 往後移動,同時把 <code>3</code> 指派給新 <code>validIndex</code>,此時因為 <code>index</code> 已經到達數組末尾,循環結束。
這時候得到的 <code>validIndex</code> 就是不重複數組元素的下标,用這種方式避免了數組的大量移動,僅僅通過覆寫的方式就達到了目的,下面就是雙指針的代碼實作(示例中代碼 <code>validLength</code> 初始為 <code>1</code>,是以比較的需要時候是 <code>arr[validLength - 1]</code>)需要減 <code>1</code>,而指派的時候是 <code>arr[validLength++]</code>,不需要加 <code>1</code>:
本文主要講述了資料結構中最基礎的一種資料結構數組的特性,并且分析了數組的特性決定了數組的通路是高效的,但是插入和删除是低效的原因。數組本身比較簡單,但是數組又是許多進階算法的載體,是以我們如果想要學習進階算法,那麼數組的增删改查是必須要掌握的,同時最後我們通過一個例子介紹了雙指針思想的利用,在數組中的相關操作中,利用雙指針可以巧妙的避免操作數組時帶來的大量元素移動。