購物籃分析(market basket analysis)是用來挖掘消費者已購買的或儲存在購物車中物品組合規律的方法。這個概念适用于不同的應用,特别是商店營運。源資料集是一個巨大的資料記錄,購物籃分析的目的發現源資料集中不同項之間的關聯關系。
購物籃模型是說明購物籃和其關聯的商品之間的關系的模型。來自其他研究領域的許多任務與該模型有共同點。總言之,購物籃模型可作為研究的一個最典型的例子。
購物籃也稱為事務資料集,它包含屬于同一個項集的項集合。
apriori算法是逐層挖掘項集的算法。與apriori算法不同,eclat算法是基于事務辨別項集合交集的tid集合交集項集的挖掘算法,而fp-growth算法是基于頻繁模式樹的算法。tid集合表示交易記錄辨別号的集合。
作為常見的算法設計政策,apriori算法挖掘關聯規則可以分解為以下兩個子問題:
頻繁項集生成
關聯規則生成
該分解政策大大降低了關聯規則挖掘算法的搜尋空間。
作為apriori算法的輸入,首先需要将原始輸入項集進行二值化,也就是說,1代表項集中包含有某項,0代表不包含某項。預設假設下,項集的平均大小是比較小的。流行的處理方法是将輸入資料集中的每個唯一的可用項映射為唯一的整數id。
項集通常存儲在資料庫或檔案中并需要多次掃描。為控制算法的效率,需要控制掃描的次數。在此過程中,當項集掃描其他項集時,需要對感興趣的每個項集的表示形式計數并存儲,以便算法後面使用。
在研究中,發現項集中有一個單調性特征。這說明每個頻繁項集的子集也是頻繁的。利用該性質,可以對apriori算法過程中的頻繁項集的搜尋空間進行剪枝。該性質也可以用于壓縮與頻繁項集相關的資訊。這個性質使頻繁項集内的小頻繁項集一目了然。例如,從頻繁3項集中可以輕松地找出包含的3個頻繁2項集。
購物籃模型表采用水準格式,它包含一個事務id和多個項,它是apriori算法的基本輸入格式。相反,還有另一種格式稱為垂直格式,它使用項id和一系列事務id的集合。垂直格式資料的挖掘算法留作練習。
在apriori算法頻繁項集産生過程中,主要包含以下兩種操作:連接配接和剪枝。
一個主要的假定是:任何項集中的項是按字母序排列的。
連接配接:給定頻繁k-1項集lk-1,為發現頻繁k項集lk,需要首先産生候選k項集(記為ck)。
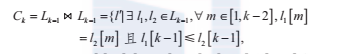
剪枝:候選項集ck通常包含頻繁項集lkck,為減少計算開銷。這裡利用單調性質對ck進行剪枝。
以下是頻繁項集産生的僞代碼:
這裡給出apriori頻繁項生成集算法的r語言代碼。記事務資料集為d,最小支援計數門檻值為min_sup,算法的輸出為l,它是資料集d中的頻繁項集。
apriori函數的輸出可以用r添加包arules來驗證,該包可以實作包含apriori算法和eclat算法的模式挖掘和關聯規則挖掘。apriori算法的r代碼如下:
為了檢驗上面的r代碼,可以應用arules添加包對算法輸出進行驗證。
給定項集:
首先,利用預先定義的排序算法将d中的項組織為有序清單,這裡,簡單地根據字母順序将各項進行排序,可得到:
假定最小支援計數為5,輸入資料如下表所示:
在對資料集d的第一次掃描中,可以得到每個候選1項集c1的支援計數。候選項集及其支援計數為:
在将支援計數與最小支援計數比較後,可以得到頻繁1項集l1:
通過l1,産生候選項集c2,c2={{i1, i2}, {i1, i4}, {i2, i4}}。
将支援計數與最小支援數比較後,可以得到l2=?。然後,算法終止。
為提升apriori算法的效率和可擴充性,人們提出了apriori算法的一些變體。下面介紹幾種比較代表性的apriori改進算法。
apriori算法循環的次數與模式的最大長度是一樣的。eclat(equivalence class transformation)算法是為了減少循環次數而設計的算法。在eclat算法中,資料格式不再是(<事務編号,項id集合>),而是(<項id,事務編号集合>)。eclat算法的資料輸入格式是樣本購物籃檔案中的垂直格式,或者從事務資料集中發現頻繁項集。在該算法中,還使用apriori性質從k項集生成頻繁k+1項集。
通過求集合的交集來生成候選項集。正如前文所述,垂直格式結構稱為事務編号集合(tidset)。如果與某個項目i相關的所有事務編号都存儲在一個垂直格式事務集合中,那麼該項集就是特定項的事務編号集合。
通過求事務編号集合的交集來計算支援計數。給定兩個tidset x和y,x∩y交集的支援計數是x∩y的基數。僞代碼是f←, p←{|i∈i, |t(i)|≥min_sup}。
下面給出eclat算法挖掘頻繁模式的r語言代碼。在調用該函數前,需要将f設為空,而p是頻繁1項集。
這裡給出一個例子的運作結果。其中,i={beer,chips,pizza,wine}。與之對應的水準和垂直格式的事務資料集如下表所示。
該資訊的二進制格式為:
在調用eclat算法之前,設定最小支援度min_sup=2, f={},則有:
算法運作過程如下圖所示。經過兩次疊代後,可以得到所有的頻繁事物編号集合,{,,,,<{beer, chips}, 1 2>}。
可以使用r添加包arules對eclat函數的結果進行驗證。
fp-growth算法是在大資料集中挖掘頻繁項集的高效算法。fp-growth算法與apriori算法的最大差別在于,該算法不需要生成候選項集,而是使用模式增長政策。頻繁模式(fp)樹是一種資料結構。
算法采用一種垂直和水準資料集混合的資料結構,所有的事務項集存儲在樹結構中。該算法使用的樹結構稱為頻繁模式樹。這裡,給出了該結構生成的一個例子。其中,i={a,b,c,d,e,f},事務資料集d如下表所示。fp樹的建構過程如下表所示。fp樹中的每個節點表示一個項目以及從根節點到該節點的路徑,即節點清單表示一個項集。這個項集以及項集的支援資訊包含在每個節點中。
排序的項目順序如下表所示。
根據這個新的降序順序,對事務資料集進行重新記錄,生成新的有序事務資料集,如下表所示:
随着将每個項集添加到fp樹中,可生成最終的fp樹,fp樹的生成過程如下圖所示。在頻繁模式(fp)樹生成過程中,同時計算各項的支援資訊,即随着節點添加到頻繁模式樹的同時,到節點路徑上的項目的支援計數也随之增加。
将最頻繁項放置在樹的頂部,這樣可以使樹盡可能緊湊。為了開始建立頻繁模式樹,首先按照支援計數降序的方式對項進行排序。其次,得到項的有序清單并删除不頻繁項。然後,根據這個順序對原始事務資料集中的每個項重新排序。
給定最小支援度min_sup=3,根據這個邏輯可以對下面的項集進行處理。
下面是執行步驟4和步驟7後的結果,算法的過程非常簡單和直接。
頭表通常與頻繁模式樹結合在一起。頭指針表的每個記錄存儲指向特定節點或項目的連結。
作為fp-growth算法的輸入,頻繁模式樹用來發現頻繁模式或頻繁項集。這裡的例子是以逆序或從葉子節點删除fp樹的項目,是以,順序是a, b, c, d, e。按照這種順序,可以為每個項目建立投影頻繁模式樹。
這裡是遞歸定義的僞代碼,其輸入值為:r←generatefptree(d), p← , f←
2.2.4.3 r語言實作
fp-growth算法的主要部分的r語言實作代碼如下所示。
genmax算法用來挖掘最大頻繁項集(maximal frequent itemset,mfi)。算法應用了最大性特性,即增加多步來檢查最大頻繁項集而不隻是頻繁項集。這部分基于eclat算法的事物編号集合交集運算。差集用于快速頻繁檢驗。它是兩個對應項目的事物編号集合的差。
可以通過候選最大頻繁項集的定義來确定它。假定最大頻繁項集記為m,若x屬于m,且x是新得到頻繁項集y的超集,則y被丢棄;然而,若x是y的子集,則将x從集合m中移除。
下面是調用genmax算法前的僞代碼,
m← ,且p←{|xi∈d, support_count(xi)≥min_sup}
其中,d是輸入事務資料集。
genmax算法的主要部分的r語言代碼如下所示:
在挖掘頻繁閉項集過程中,需要對項集進行封閉檢查。通過頻繁閉項集,可以得到具有相同支援度的最大頻繁模式。這樣可以對備援的頻繁模式進行剪枝。charm算法還利用垂直事物編号集合的交集運算來進行快速的封閉檢查。
下面是調用charm算法前的僞代碼,
c← ,且p←{|xi∈d, support_count(xi)≥min_sup}
charm算法的主要部分的r語言實作代碼如下:
在根據apriori算法生成頻繁項集的過程中,計算并儲存每個頻繁項集的支援計數以便用于後面的關聯規則挖掘過程,即關聯規則挖掘。
為生成關聯規則x→y,l=x∪y,l為某個頻繁項集,需要以下兩個步驟:
首先,得到l的所有非空子集。
然後,對于l的子集x,y=l-x,規則x→y為強關聯規則,當且僅當confidence(x→y)≥minimumconfidence。一個頻繁項集的任何規則的支援計數不能小于最小支援計數。
關聯規則生成算法的僞代碼如下所示。
生成apriori關聯規則的算法的r語言代碼如下所示:
為了驗證上述r語言代碼,可以使用arules和rattle添加包驗證它的輸出。