购物篮分析(market basket analysis)是用来挖掘消费者已购买的或保存在购物车中物品组合规律的方法。这个概念适用于不同的应用,特别是商店运营。源数据集是一个巨大的数据记录,购物篮分析的目的发现源数据集中不同项之间的关联关系。
购物篮模型是说明购物篮和其关联的商品之间的关系的模型。来自其他研究领域的许多任务与该模型有共同点。总言之,购物篮模型可作为研究的一个最典型的例子。
购物篮也称为事务数据集,它包含属于同一个项集的项集合。
apriori算法是逐层挖掘项集的算法。与apriori算法不同,eclat算法是基于事务标识项集合交集的tid集合交集项集的挖掘算法,而fp-growth算法是基于频繁模式树的算法。tid集合表示交易记录标识号的集合。
作为常见的算法设计策略,apriori算法挖掘关联规则可以分解为以下两个子问题:
频繁项集生成
关联规则生成
该分解策略大大降低了关联规则挖掘算法的搜索空间。
作为apriori算法的输入,首先需要将原始输入项集进行二值化,也就是说,1代表项集中包含有某项,0代表不包含某项。默认假设下,项集的平均大小是比较小的。流行的处理方法是将输入数据集中的每个唯一的可用项映射为唯一的整数id。
项集通常存储在数据库或文件中并需要多次扫描。为控制算法的效率,需要控制扫描的次数。在此过程中,当项集扫描其他项集时,需要对感兴趣的每个项集的表示形式计数并存储,以便算法后面使用。
在研究中,发现项集中有一个单调性特征。这说明每个频繁项集的子集也是频繁的。利用该性质,可以对apriori算法过程中的频繁项集的搜索空间进行剪枝。该性质也可以用于压缩与频繁项集相关的信息。这个性质使频繁项集内的小频繁项集一目了然。例如,从频繁3项集中可以轻松地找出包含的3个频繁2项集。
购物篮模型表采用水平格式,它包含一个事务id和多个项,它是apriori算法的基本输入格式。相反,还有另一种格式称为垂直格式,它使用项id和一系列事务id的集合。垂直格式数据的挖掘算法留作练习。
在apriori算法频繁项集产生过程中,主要包含以下两种操作:连接和剪枝。
一个主要的假定是:任何项集中的项是按字母序排列的。
连接:给定频繁k-1项集lk-1,为发现频繁k项集lk,需要首先产生候选k项集(记为ck)。
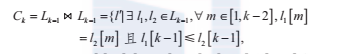
剪枝:候选项集ck通常包含频繁项集lkck,为减少计算开销。这里利用单调性质对ck进行剪枝。
以下是频繁项集产生的伪代码:
这里给出apriori频繁项生成集算法的r语言代码。记事务数据集为d,最小支持计数阈值为min_sup,算法的输出为l,它是数据集d中的频繁项集。
apriori函数的输出可以用r添加包arules来验证,该包可以实现包含apriori算法和eclat算法的模式挖掘和关联规则挖掘。apriori算法的r代码如下:
为了检验上面的r代码,可以应用arules添加包对算法输出进行验证。
给定项集:
首先,利用预先定义的排序算法将d中的项组织为有序列表,这里,简单地根据字母顺序将各项进行排序,可得到:
假定最小支持计数为5,输入数据如下表所示:
在对数据集d的第一次扫描中,可以得到每个候选1项集c1的支持计数。候选项集及其支持计数为:
在将支持计数与最小支持计数比较后,可以得到频繁1项集l1:
通过l1,产生候选项集c2,c2={{i1, i2}, {i1, i4}, {i2, i4}}。
将支持计数与最小支持数比较后,可以得到l2=?。然后,算法终止。
为提升apriori算法的效率和可扩展性,人们提出了apriori算法的一些变体。下面介绍几种比较代表性的apriori改进算法。
apriori算法循环的次数与模式的最大长度是一样的。eclat(equivalence class transformation)算法是为了减少循环次数而设计的算法。在eclat算法中,数据格式不再是(<事务编号,项id集合>),而是(<项id,事务编号集合>)。eclat算法的数据输入格式是样本购物篮文件中的垂直格式,或者从事务数据集中发现频繁项集。在该算法中,还使用apriori性质从k项集生成频繁k+1项集。
通过求集合的交集来生成候选项集。正如前文所述,垂直格式结构称为事务编号集合(tidset)。如果与某个项目i相关的所有事务编号都存储在一个垂直格式事务集合中,那么该项集就是特定项的事务编号集合。
通过求事务编号集合的交集来计算支持计数。给定两个tidset x和y,x∩y交集的支持计数是x∩y的基数。伪代码是f←, p←{|i∈i, |t(i)|≥min_sup}。
下面给出eclat算法挖掘频繁模式的r语言代码。在调用该函数前,需要将f设为空,而p是频繁1项集。
这里给出一个例子的运行结果。其中,i={beer,chips,pizza,wine}。与之对应的水平和垂直格式的事务数据集如下表所示。
该信息的二进制格式为:
在调用eclat算法之前,设置最小支持度min_sup=2, f={},则有:
算法运行过程如下图所示。经过两次迭代后,可以得到所有的频繁事物编号集合,{,,,,<{beer, chips}, 1 2>}。
可以使用r添加包arules对eclat函数的结果进行验证。
fp-growth算法是在大数据集中挖掘频繁项集的高效算法。fp-growth算法与apriori算法的最大区别在于,该算法不需要生成候选项集,而是使用模式增长策略。频繁模式(fp)树是一种数据结构。
算法采用一种垂直和水平数据集混合的数据结构,所有的事务项集存储在树结构中。该算法使用的树结构称为频繁模式树。这里,给出了该结构生成的一个例子。其中,i={a,b,c,d,e,f},事务数据集d如下表所示。fp树的构建过程如下表所示。fp树中的每个节点表示一个项目以及从根节点到该节点的路径,即节点列表表示一个项集。这个项集以及项集的支持信息包含在每个节点中。
排序的项目顺序如下表所示。
根据这个新的降序顺序,对事务数据集进行重新记录,生成新的有序事务数据集,如下表所示:
随着将每个项集添加到fp树中,可生成最终的fp树,fp树的生成过程如下图所示。在频繁模式(fp)树生成过程中,同时计算各项的支持信息,即随着节点添加到频繁模式树的同时,到节点路径上的项目的支持计数也随之增加。
将最频繁项放置在树的顶部,这样可以使树尽可能紧凑。为了开始创建频繁模式树,首先按照支持计数降序的方式对项进行排序。其次,得到项的有序列表并删除不频繁项。然后,根据这个顺序对原始事务数据集中的每个项重新排序。
给定最小支持度min_sup=3,根据这个逻辑可以对下面的项集进行处理。
下面是执行步骤4和步骤7后的结果,算法的过程非常简单和直接。
头表通常与频繁模式树结合在一起。头指针表的每个记录存储指向特定节点或项目的链接。
作为fp-growth算法的输入,频繁模式树用来发现频繁模式或频繁项集。这里的例子是以逆序或从叶子节点删除fp树的项目,因此,顺序是a, b, c, d, e。按照这种顺序,可以为每个项目创建投影频繁模式树。
这里是递归定义的伪代码,其输入值为:r←generatefptree(d), p← , f←
2.2.4.3 r语言实现
fp-growth算法的主要部分的r语言实现代码如下所示。
genmax算法用来挖掘最大频繁项集(maximal frequent itemset,mfi)。算法应用了最大性特性,即增加多步来检查最大频繁项集而不只是频繁项集。这部分基于eclat算法的事物编号集合交集运算。差集用于快速频繁检验。它是两个对应项目的事物编号集合的差。
可以通过候选最大频繁项集的定义来确定它。假定最大频繁项集记为m,若x属于m,且x是新得到频繁项集y的超集,则y被丢弃;然而,若x是y的子集,则将x从集合m中移除。
下面是调用genmax算法前的伪代码,
m← ,且p←{|xi∈d, support_count(xi)≥min_sup}
其中,d是输入事务数据集。
genmax算法的主要部分的r语言代码如下所示:
在挖掘频繁闭项集过程中,需要对项集进行封闭检查。通过频繁闭项集,可以得到具有相同支持度的最大频繁模式。这样可以对冗余的频繁模式进行剪枝。charm算法还利用垂直事物编号集合的交集运算来进行快速的封闭检查。
下面是调用charm算法前的伪代码,
c← ,且p←{|xi∈d, support_count(xi)≥min_sup}
charm算法的主要部分的r语言实现代码如下:
在根据apriori算法生成频繁项集的过程中,计算并保存每个频繁项集的支持计数以便用于后面的关联规则挖掘过程,即关联规则挖掘。
为生成关联规则x→y,l=x∪y,l为某个频繁项集,需要以下两个步骤:
首先,得到l的所有非空子集。
然后,对于l的子集x,y=l-x,规则x→y为强关联规则,当且仅当confidence(x→y)≥minimumconfidence。一个频繁项集的任何规则的支持计数不能小于最小支持计数。
关联规则生成算法的伪代码如下所示。
生成apriori关联规则的算法的r语言代码如下所示:
为了验证上述r语言代码,可以使用arules和rattle添加包验证它的输出。