1.本周學習總結
1.思維導圖
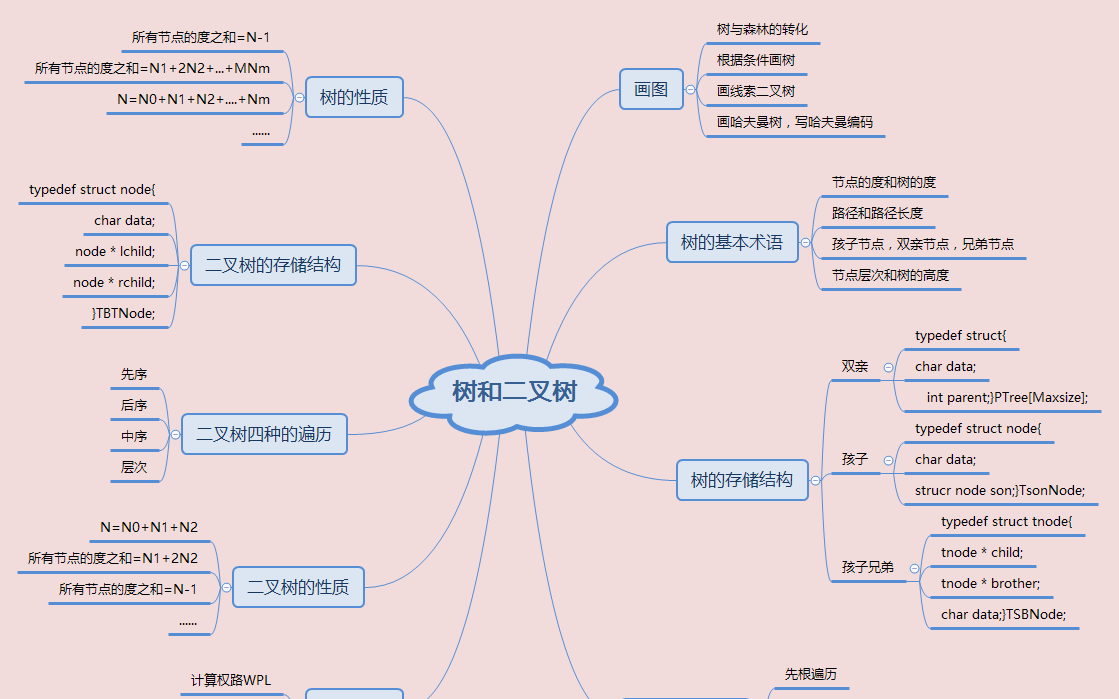
2.談談你對樹結構的認識及學習體會
- 對于樹學到了樹的多種存儲結構,孩子樹,雙親樹,孩子兄弟樹,二叉樹,結構體中的内容差不多都是值和指針的組合,但是也各有個的優缺點,比如孩子樹找孩子十分友善找雙親就困難,空指針域也較多比較浪費等。對于樹的操作一般從建樹開始,然後周遊,周遊又分為多種順序的周遊,比如二叉樹的周遊就有四種,其中先序中序後序周遊可用遞歸完成,其後就是一些求高度求寬度找路徑,插入删除的操作。
- 關于樹的學習,我覺得要記住的内容有點多,樹的基本術語,樹的性質,好多條沒有好記性記了好久一直忘記或記錯,還有就是畫樹的課堂派題目,用畫圖軟體畫真的很費時間,一題能畫半個小時,最近這兩周的時間比較不夠選修課有大作業,樹有大作業又要複習機率,又有實體實驗,幾乎沒時間寫pta ,題目真的寫得少,然後不知不覺樹學完了。
2.PTA實驗作業
2.1.題目1:表達式樹
2.1.1設計思路(僞代碼)
建表達式的二叉樹函數
op.push('#');
while str[i] then
if !In(str[i]) then//不是運算符
T=new BTNode;
T->data=str[i++];
左右孩子為空
T入棧
end if
else//是運算符
switch Precede(op.top(),str[i])//優先級的比較
case'<':
進棧
case'=':
出棧
case'>':
建一個節點,值為符号棧頂,
左右孩子分别為資料棧頂
T->rchild=digit.top();
digit.pop();
T->lchild=digit.top()
digit.pop();
T入棧
end swith
end else
end while
while op.top()!='#' then
同 case'>'的情況
end while
T=digit.top();
}
計算表達式樹函數
if !T->rchild&&!T->lchild then//遞歸口
return T->data-'0';
end if
item1=EvaluateExTree(T->lchild);
item2同上
switch T->data//運算符的處理
case'+':
return item1+item2;
break;
"-"和"*"同上
case'/':
if item2==0 then//分母為0的情況
cout<<"divide 0 error!";
exit(0);
end if
return item1/item2;
break;
end swith
2.1.2代碼截圖
2.1.3本題PTA送出清單說明
問題1:用測試樣例試沒問題,用自己想的資料沒問題,都快懷疑人生了。
解決1:
,加break真的很重要。
問題2:一直段錯誤,改了好久。
解決2:用慣了for循環while循環的時候沒有i++,而且還忘了出棧,找了半天問題所在。
2.2.題目2:二叉樹葉子結點帶權路徑長度和
2.2.1設計思路(僞代碼)
typedef struct BTNode* BTree;
struct BTNode
{
char data;
BTree lchild;
BTree rchild;
};
建樹函數
BTree T;
if i大于str的長度-1或str[i]等于#号 then
return NULL;
end if
T=new BTNode;
T->data=str[i];
T->lchild=CreateBTree(2*i,str);
T->rchild=CreateBTree(2*i+1,str);
return T;
獲得WPL函數
if T==NULL then
return;
if 左右孩子皆為空 then
wpl=wpl+h*(T->data-'0');
h=0;
end if
h++;
GetWpl(T->lchild,wpl,h);
GetWpl(T->rchild,wpl,h);
主函數
string str;
BTree T;
int i=1;
int wpl=0;
int h=0;
輸入str
T=CreateBTree(i,str);
GetWpl(T,wpl,h);
輸出wpl
return 0;
2.2.2代碼截圖
2.2.3本題PTA送出清單說明
問題1:發現總是少了一層的值
解決1:讓h=0就可以了,不能從h=1開始
問題2:樣例2過不了
解決2:i要控制好,是str的長度-1
2.3.題目3:輸出二叉樹每層節點
2.3.1設計思路(僞代碼)
typedef struct TNode * BinTree;
struct TNode{
char Data;
BinTree lchild;
BinTree rchild;
};
建樹函數
BinTree bt;
if i大于str的長度-1或str[i]等于#号 then
return NULL;
end if
bt = new TNode;
bt->Data = str[i];
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
return bt;
層次周遊函數
queue<BinTree> qt;
int level=0;
BinTree curNode,lastNode;
curNode=lastNode=BT;
if BT為空 then
cout<<"NULL";
return ;
end if
else
BT入棧
end else
while qt非空
if curNode等于lastNode
level++;
if level==1 then//第一行
cout<<level<<":";
end if
else//其餘行
cout<<endl<<level<<":";
end else
lastNode=qt.back();
end if
curNode=qt.front();
cout<<curNode->Data<<",";//格式
if curNode->lchild非空 then
qt.push(curNode->lchild);
end if
curNode->rchild 同上
qt.pop();
end while
主函數
char str[100];
BinTree BT;
int i=0;
cin>>str;
BT=CreatTree(str,i);
LevelOrder(BT);
2.3.2代碼截圖
2.3.3本題PTA送出清單說明
問題1:關于層次周遊不知道什麼時候是一層結束
解決1:通過上課老師講評知道curNode等于lastNode時一層結束,繼續下一層
3.閱讀代碼
3.1 題目
給出一棵二叉樹,其上每個結點的值都是 0 或 1 。每一條從根到葉的路徑都代表一個從最高有效位開始的二進制數。例如,如果路徑為 0 -> 1 -> 1 -> 0 -> 1,那麼它表示二進制數 01101,也就是 13 。
示例:
輸入:[1,0,1,0,1,0,1]
輸出:22
解釋:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
3.2 解題思路
- 這是一顆二叉樹,從根節點開始周遊,每向下一個節點,我們可以把父節點傳入的值進一位并加上目前節點的值。這樣我們就得到了一個從根節點到目前節點表示的數值。接下來我們要做的隻是判斷一個節點是不是葉子節點,如果是的話就累加進入sumRootToLeaf函數,傳回,否則繼續sumRootToLeaf_sub函數。
3.3 代碼截圖
3.4 學習體會
- 這段代碼運用了多個遞歸,在非葉子節點一直運用sumRootToLeaf_sub函數進行計算,效率挺高的,每個節點周遊一次,時間複雜度O(N),不需要額外的存儲空間,空間複雜度O(1).其中的代碼
last = last * 2 + root->val;
last = last <<1 | root->val;
轉載于:https://www.cnblogs.com/linshuxin1761/p/10885544.html