歐拉回路、鍊路

一，歐拉回路、歐拉鍊路

二，無向圖

三，有向圖

四，Hierholzer算法

1，遞歸版

力扣 332. 重新安排行程（有向圖的歐拉鍊路）

力扣 753. 破解保險箱（有向圖的歐拉回路）

2，非遞歸版

力扣 2097. 合法重新排列數對（有向圖的歐拉回路或鍊路）

一，歐拉回路、歐拉鍊路

從起點A出發，不重複的走完所有的邊，最終回到A，得到的回路叫歐拉回路。

從起點A出發，不重複的走完所有的邊，到達終點B，得到的鍊路叫歐拉鍊路。

尋找歐拉回路或者歐拉鍊路就是經典的一筆畫問題。

二，無向圖

對于無向連通圖，存在歐拉回路的充要條件是奇點數量為0，存在歐拉鍊路的充要條件是奇點數量為2。

換句話說，如果奇點數量大于2則無法一筆畫。

三，有向圖

對于有向圖G，存在歐拉回路的充要條件是，G是強連通圖且所有節點的入度都等于出度。

對于有向圖G，存在歐拉鍊路的充要條件是，G是半連通圖且隻有2個節點的出度-入度=正負1，其他節點都滿足入度都等于出度。

四，Hierholzer算法

1，遞歸版

Hierholzer算法求歐拉回路或鍊路就是從任意一點開始進行dfs周遊所有的邊，把周遊結束的點入棧，最終得到的就是歐拉回路，棧頂就是起點。

class Hierholzer {
public:
  stack<int>euler;//歐拉回路或鍊路,棧頂是起點
  Hierholzer(int n, map<int, vector<int>>& m,int type,int start=0)//type=0是無向圖 1是有向圖
  {
    this->n = n;
    this->m = m;
    this->type = type;
    dfs(GetStartPoint(start));
  }
private:
  int GetStartPoint(int start)//鍊路是唯一起點，回路是指定起點
  {
    if (type == 0) {
      for (auto& mi : m) {
        if (mi.second.size() % 2)return mi.first;
        for (auto nk : mi.second)num[id(mi.first, nk)]++;
      }
      for (auto& ni : num)ni.second /= 2;
    } else {
      map<int, int>m2;
      for (auto& mi : m)for (auto nk : mi.second)m2[nk]++, num[id(mi.first, nk)]++;
      for (auto& mi : m)if (mi.second.size() > m2[mi.first])return mi.first;
    }
    return start;
  }
  void dfs(int k)
  {
    for (auto nk : m[k]) {
      if (num[id(k, nk)]--<=0)continue;
      dfs(nk);
    }
    euler.push(k);
  }
  long long id(int a, int b)
  {
    if (type == 0 && a > b)a ^= b ^= a ^= b;
    return (long long)a * n + b;
  }
  int n;
  int type;
  map<int, vector<int>> m;//鄰接表
  map<long long, int>num;//支援多重邊
};

這份代碼能同時适用于無向圖和有向圖，自動判斷是求歐拉回路還是鍊路，并以棧作為傳回值。

另外一個優點是支援多重邊。

缺點是沒有做校驗是否存在歐拉回路或鍊路。

力扣 332. 重新安排行程（有向圖的歐拉鍊路）

給你一份航線清單

tickets

，其中

tickets[i] = [fromi, toi]

表示飛機出發和降落的機場地點。請你對該行程進行重新規劃排序。

所有這些機票都屬于一個從

JFK

（肯尼迪國際機場）出發的先生，是以該行程必須從

JFK

開始。如果存在多種有效的行程，請你按字典排序傳回最小的行程組合。

例如，行程 ["JFK", "LGA"] 與 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有機票至少存在一種合理的行程。且所有的機票必須都用一次且隻能用一次。

示例 1：

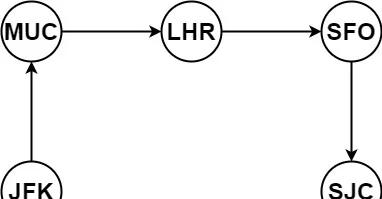
輸入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]

輸出：["JFK","MUC","LHR","SFO","SJC"]

示例 2：

輸入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]

輸出：["JFK","ATL","JFK","SFO","ATL","SFO"]

解釋：另一種有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠後。

提示：

1 <= tickets.length <= 300
tickets[i].length == 2
fromi.length == 3
toi.length == 3
fromi 和 toi 由大寫英文字母組成
fromi != toi

題意：

給一個帶多重邊的有向圖，指定起點，求歐拉鍊路。

class Solution {
public:
  vector<string> findItinerary(vector<vector<string>>& tickets) {
    vector<string>v;
    map<string, int>m;
    for (auto& ti : tickets)m[ti[0]],m[ti[1]];
    for (auto& mi : m)v.push_back(mi.first);
    sort(v.begin(), v.end());
    m.clear();
    for (int i = 0; i < v.size(); i++)m[v[i]] = i;
    map<int, vector<int>>g;
    for (auto& ti : tickets)g[m[ti[0]]].push_back(m[ti[1]]);
    for (auto& gi : g)sort(gi.second.begin(), gi.second.end());
    stack<int>s = Hierholzer(v.size(), g, 1, m["JFK"]).euler;
    vector<string> ans;
    while (!s.empty())ans.push_back(v[s.top()]), s.pop();
    return ans;
  }
};

力扣 753. 破解保險箱（有向圖的歐拉回路）

有一個需要密碼才能打開的保險箱。密碼是 n 位數, 密碼的每一位是 k 位序列 0, 1, ..., k-1 中的一個。

你可以随意輸入密碼，保險箱會自動記住最後 n 位輸入，如果比對，則能夠打開保險箱。

舉個例子，假設密碼是 "345"，你可以輸入 "012345" 來打開它，隻是你輸入了 6 個字元.

請傳回一個能打開保險箱的最短字元串。

示例1:

輸入: n = 1, k = 2

輸出: "01"

說明: "10"也可以打開保險箱。

示例2:

輸入: n = 2, k = 2

輸出: "00110"

說明: "01100", "10011", "11001" 也能打開保險箱。

提示：

n 的範圍是 [1, 4]。

k 的範圍是 [1, 10]。

k^n 最大可能為 4096。

思路：

以前n-1位密碼的所有可能性作為點，以最後一位作為邊，那麼保險箱的枚舉密碼就可以表示成求歐拉回路或鍊路。

節點數量是pow(k, n - 1)，邊的數量是pow(k, n)

實際上，由于對稱性，求的是歐拉回路。

class Solution {
public:
  string crackSafe(int n, int k) {
    if (n == 1) {
      string str(k, '0');
      for (int i = 0; i < str.size(); i++)str[i] += i;
      return str;
    }
    map<int, vector<int>>m;
    int num = pow(k, n - 1);
    for (int i = 0; i < num; i++) {
      for (int j = 0; j < k; j++)m[i].push_back(i % (num / k)*k + j);
    }
    auto s = Hierholzer(m.size(), m, 1).euler;
    string str(num * k + n - 1, '0');
    int id = 0, t = s.top();
    char c = '0';
    s.pop();
    for (int i = 0; i < n - 1; i++)str[id++] = c + s.top() % k, t /= k;
    while (!s.empty())str[id++] = c + s.top() % k, s.pop();
    return str;
  }
};

2，非遞歸版

為了克服遞歸太深導緻爆棧的問題，我把算法改寫成非遞歸版，功能和接口都不變。

class Hierholzer {
public:
  stack<int>euler;//歐拉回路或鍊路,棧頂是起點
  Hierholzer(int n, map<int, vector<int>>& m,int type,int start=0)//type=0是無向圖 1是有向圖
  {
    this->n = n;
    this->m = m;
    this->type = type;
    dfs(GetStartPoint(start));
  }
private:
  int GetStartPoint(int start)//鍊路是唯一起點，回路是指定起點
  {
    if (type == 0) {
      for (auto& mi : m) {
        if (mi.second.size() % 2)return mi.first;
        for (auto nk : mi.second)num[id(mi.first, nk)]++;
      }
      for (auto& ni : num)ni.second /= 2;
    } else {
      map<int, int>m2;
      for (auto& mi : m)for (auto nk : mi.second)m2[nk]++, num[id(mi.first, nk)]++;
      for (auto& mi : m)if (mi.second.size() > m2[mi.first])return mi.first;
    }
    return start;
  }
  void dfs(int k)
  {
    while (true) {
      while (mid[k] < m[k].size()) {
        if (num[id(k, m[k][mid[k]])]-- <= 0)mid[k]++;
        else sdfs.push(k), k = m[k][mid[k]];
      }
      euler.push(k);
      if (sdfs.empty()) return;
      k = sdfs.top(), sdfs.pop();
    }
  }
  inline long long id(int a, int b)
  {
    if (type == 0 && a > b)a ^= b ^= a ^= b;
    return (long long)a * n + b;
  }
  int n;
  int type;
  stack<int>sdfs;
  map<int, vector<int>> m;//鄰接表
  map<int, int>mid;
  map<long long, int>num;//支援多重邊
};

力扣 2097. 合法重新排列數對（有向圖的歐拉回路或鍊路）

給你一個下标從 0 開始的二維整數數組

pairs

，其中

pairs[i] = [starti, endi]

。如果

pairs

的一個重新排列，滿足對每一個下标

（

1 <= i < pairs.length

）都有

endi-1 == starti

，那麼我們就認為這個重新排列是

pairs

的一個合法重新排列。

請你傳回任意一個

pairs

的合法重新排列。

注意：資料保證至少存在一個

pairs

的合法重新排列。

示例 1：

輸入：pairs = [[5,1],[4,5],[11,9],[9,4]]

輸出：[[11,9],[9,4],[4,5],[5,1]]

解釋：

輸出的是一個合法重新排列，因為每一個 endi-1 都等于 starti 。

end0 = 9 == 9 = start1

end1 = 4 == 4 = start2

end2 = 5 == 5 = start3

示例 2：

輸入：pairs = [[1,3],[3,2],[2,1]]

輸出：[[1,3],[3,2],[2,1]]

解釋：

輸出的是一個合法重新排列，因為每一個 endi-1 都等于 starti 。

end0 = 3 == 3 = start1

end1 = 2 == 2 = start2

重新排列後的數組 [[2,1],[1,3],[3,2]] 和 [[3,2],[2,1],[1,3]] 都是合法的。

示例 3：

1 <= pairs.length <= 105
pairs[i].length == 2
0 <= starti, endi <= 109
starti != endi
pairs 中不存在一模一樣的數對。
至少存在一個合法的 pairs 重新排列。

class Solution {
public:
  vector<vector<int>> validArrangement(vector<vector<int>>& pairs) {
    map<int, vector<int>>g;
    for (auto& p : pairs)g[p[0]].push_back(p[1]);
    stack<int>s = Hierholzer(g.size(), g, 1, pairs[0][0]).euler;
    int a = s.top(), b;
    s.pop();
    vector<vector<int>>ans(s.size());
    for(int i=0;i<ans.size();i++) {
      b = s.top();
      ans[i] = vector<int>{ a, b };
      a = b;
      s.pop();
    }
    return ans;
  }
};

歐拉回路、鍊路

一，歐拉回路、歐拉鍊路

二，無向圖

三，有向圖

四，Hierholzer算法

1，遞歸版

力扣 332. 重新安排行程（有向圖的歐拉鍊路）

力扣 753. 破解保險箱（有向圖的歐拉回路）

2，非遞歸版

力扣 2097. 合法重新排列數對（有向圖的歐拉回路或鍊路）

繼續閱讀

Codeforces 1417 D. Make Them Equal(思維+構造)

查找算法之二分查找查找算法之二分查找

查找算法學習之二分查找（Python版本）——BinarySearch

CQ V1.0分詞bates(基于雙數組tire樹)—應該是目前最快的中文分詞算法

Command Network(POJ 3164)---定根最小樹形圖模闆題題目描述輸入格式輸出格式輸入樣例輸出樣例分析源程式

開源低帶寬語音編解碼器

241 Different Ways to Add Parentheses（C代碼版）

【趨高機器視覺】機器視覺技術原了解析及解決方案

CSMA/CD1． CSMA/CD的概述2． CSMA 的工作原理3． CSMA/CD控制規程及特點4． CSMA/CD協定5． CSMA/CD的優點6．結束語

極大似然法(ML)與最大期望法(EM)

C++ 第十五周報告1--《冒泡法排序》

筆試面試題目：滑動視窗(二)

資料結構與算法（27）——排序（二）

Dijkstra--簡易版（最短路徑）

GitHub連夜封殺！這份阿裡 10W 字内部 Java 字面試手冊到底有多強？

hdu7108哈希