欧拉回路、链路

一，欧拉回路、欧拉链路

二，无向图

三，有向图

四，Hierholzer算法

1，递归版

力扣 332. 重新安排行程（有向图的欧拉链路）

力扣 753. 破解保险箱（有向图的欧拉回路）

2，非递归版

力扣 2097. 合法重新排列数对（有向图的欧拉回路或链路）

一，欧拉回路、欧拉链路

从起点A出发，不重复的走完所有的边，最终回到A，得到的回路叫欧拉回路。

从起点A出发，不重复的走完所有的边，到达终点B，得到的链路叫欧拉链路。

寻找欧拉回路或者欧拉链路就是经典的一笔画问题。

二，无向图

对于无向连通图，存在欧拉回路的充要条件是奇点数量为0，存在欧拉链路的充要条件是奇点数量为2。

换句话说，如果奇点数量大于2则无法一笔画。

三，有向图

对于有向图G，存在欧拉回路的充要条件是，G是强连通图且所有节点的入度都等于出度。

对于有向图G，存在欧拉链路的充要条件是，G是半连通图且只有2个节点的出度-入度=正负1，其他节点都满足入度都等于出度。

四，Hierholzer算法

1，递归版

Hierholzer算法求欧拉回路或链路就是从任意一点开始进行dfs遍历所有的边，把遍历结束的点入栈，最终得到的就是欧拉回路，栈顶就是起点。

class Hierholzer {
public:
  stack<int>euler;//欧拉回路或链路,栈顶是起点
  Hierholzer(int n, map<int, vector<int>>& m,int type,int start=0)//type=0是无向图 1是有向图
  {
    this->n = n;
    this->m = m;
    this->type = type;
    dfs(GetStartPoint(start));
  }
private:
  int GetStartPoint(int start)//链路是唯一起点，回路是指定起点
  {
    if (type == 0) {
      for (auto& mi : m) {
        if (mi.second.size() % 2)return mi.first;
        for (auto nk : mi.second)num[id(mi.first, nk)]++;
      }
      for (auto& ni : num)ni.second /= 2;
    } else {
      map<int, int>m2;
      for (auto& mi : m)for (auto nk : mi.second)m2[nk]++, num[id(mi.first, nk)]++;
      for (auto& mi : m)if (mi.second.size() > m2[mi.first])return mi.first;
    }
    return start;
  }
  void dfs(int k)
  {
    for (auto nk : m[k]) {
      if (num[id(k, nk)]--<=0)continue;
      dfs(nk);
    }
    euler.push(k);
  }
  long long id(int a, int b)
  {
    if (type == 0 && a > b)a ^= b ^= a ^= b;
    return (long long)a * n + b;
  }
  int n;
  int type;
  map<int, vector<int>> m;//邻接表
  map<long long, int>num;//支持多重边
};

这份代码能同时适用于无向图和有向图，自动判断是求欧拉回路还是链路，并以栈作为返回值。

另外一个优点是支持多重边。

缺点是没有做校验是否存在欧拉回路或链路。

力扣 332. 重新安排行程（有向图的欧拉链路）

给你一份航线列表

tickets

，其中

tickets[i] = [fromi, toi]

表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从

JFK

（肯尼迪国际机场）出发的先生，所以该行程必须从

JFK

开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票必须都用一次且只能用一次。

示例 1：

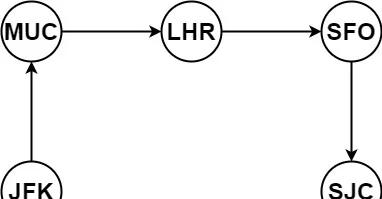
输入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]

输出：["JFK","MUC","LHR","SFO","SJC"]

示例 2：

输入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]

输出：["JFK","ATL","JFK","SFO","ATL","SFO"]

解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。

提示：

1 <= tickets.length <= 300
tickets[i].length == 2
fromi.length == 3
toi.length == 3
fromi 和 toi 由大写英文字母组成
fromi != toi

题意：

给一个带多重边的有向图，指定起点，求欧拉链路。

class Solution {
public:
  vector<string> findItinerary(vector<vector<string>>& tickets) {
    vector<string>v;
    map<string, int>m;
    for (auto& ti : tickets)m[ti[0]],m[ti[1]];
    for (auto& mi : m)v.push_back(mi.first);
    sort(v.begin(), v.end());
    m.clear();
    for (int i = 0; i < v.size(); i++)m[v[i]] = i;
    map<int, vector<int>>g;
    for (auto& ti : tickets)g[m[ti[0]]].push_back(m[ti[1]]);
    for (auto& gi : g)sort(gi.second.begin(), gi.second.end());
    stack<int>s = Hierholzer(v.size(), g, 1, m["JFK"]).euler;
    vector<string> ans;
    while (!s.empty())ans.push_back(v[s.top()]), s.pop();
    return ans;
  }
};

力扣 753. 破解保险箱（有向图的欧拉回路）

有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位是 k 位序列 0, 1, ..., k-1 中的一个。

你可以随意输入密码，保险箱会自动记住最后 n 位输入，如果匹配，则能够打开保险箱。

举个例子，假设密码是 "345"，你可以输入 "012345" 来打开它，只是你输入了 6 个字符.

请返回一个能打开保险箱的最短字符串。

示例1:

输入: n = 1, k = 2

输出: "01"

说明: "10"也可以打开保险箱。

示例2:

输入: n = 2, k = 2

输出: "00110"

说明: "01100", "10011", "11001" 也能打开保险箱。

提示：

n 的范围是 [1, 4]。

k 的范围是 [1, 10]。

k^n 最大可能为 4096。

思路：

以前n-1位密码的所有可能性作为点，以最后一位作为边，那么保险箱的枚举密码就可以表示成求欧拉回路或链路。

节点数量是pow(k, n - 1)，边的数量是pow(k, n)

实际上，由于对称性，求的是欧拉回路。

class Solution {
public:
  string crackSafe(int n, int k) {
    if (n == 1) {
      string str(k, '0');
      for (int i = 0; i < str.size(); i++)str[i] += i;
      return str;
    }
    map<int, vector<int>>m;
    int num = pow(k, n - 1);
    for (int i = 0; i < num; i++) {
      for (int j = 0; j < k; j++)m[i].push_back(i % (num / k)*k + j);
    }
    auto s = Hierholzer(m.size(), m, 1).euler;
    string str(num * k + n - 1, '0');
    int id = 0, t = s.top();
    char c = '0';
    s.pop();
    for (int i = 0; i < n - 1; i++)str[id++] = c + s.top() % k, t /= k;
    while (!s.empty())str[id++] = c + s.top() % k, s.pop();
    return str;
  }
};

2，非递归版

为了克服递归太深导致爆栈的问题，我把算法改写成非递归版，功能和接口都不变。

class Hierholzer {
public:
  stack<int>euler;//欧拉回路或链路,栈顶是起点
  Hierholzer(int n, map<int, vector<int>>& m,int type,int start=0)//type=0是无向图 1是有向图
  {
    this->n = n;
    this->m = m;
    this->type = type;
    dfs(GetStartPoint(start));
  }
private:
  int GetStartPoint(int start)//链路是唯一起点，回路是指定起点
  {
    if (type == 0) {
      for (auto& mi : m) {
        if (mi.second.size() % 2)return mi.first;
        for (auto nk : mi.second)num[id(mi.first, nk)]++;
      }
      for (auto& ni : num)ni.second /= 2;
    } else {
      map<int, int>m2;
      for (auto& mi : m)for (auto nk : mi.second)m2[nk]++, num[id(mi.first, nk)]++;
      for (auto& mi : m)if (mi.second.size() > m2[mi.first])return mi.first;
    }
    return start;
  }
  void dfs(int k)
  {
    while (true) {
      while (mid[k] < m[k].size()) {
        if (num[id(k, m[k][mid[k]])]-- <= 0)mid[k]++;
        else sdfs.push(k), k = m[k][mid[k]];
      }
      euler.push(k);
      if (sdfs.empty()) return;
      k = sdfs.top(), sdfs.pop();
    }
  }
  inline long long id(int a, int b)
  {
    if (type == 0 && a > b)a ^= b ^= a ^= b;
    return (long long)a * n + b;
  }
  int n;
  int type;
  stack<int>sdfs;
  map<int, vector<int>> m;//邻接表
  map<int, int>mid;
  map<long long, int>num;//支持多重边
};

力扣 2097. 合法重新排列数对（有向图的欧拉回路或链路）

给你一个下标从 0 开始的二维整数数组

pairs

，其中

pairs[i] = [starti, endi]

。如果

pairs

的一个重新排列，满足对每一个下标

（

1 <= i < pairs.length

）都有

endi-1 == starti

，那么我们就认为这个重新排列是

pairs

的一个合法重新排列。

请你返回任意一个

pairs

的合法重新排列。

注意：数据保证至少存在一个

pairs

的合法重新排列。

示例 1：

输入：pairs = [[5,1],[4,5],[11,9],[9,4]]

输出：[[11,9],[9,4],[4,5],[5,1]]

解释：

输出的是一个合法重新排列，因为每一个 endi-1 都等于 starti 。

end0 = 9 == 9 = start1

end1 = 4 == 4 = start2

end2 = 5 == 5 = start3

示例 2：

输入：pairs = [[1,3],[3,2],[2,1]]

输出：[[1,3],[3,2],[2,1]]

解释：

输出的是一个合法重新排列，因为每一个 endi-1 都等于 starti 。

end0 = 3 == 3 = start1

end1 = 2 == 2 = start2

重新排列后的数组 [[2,1],[1,3],[3,2]] 和 [[3,2],[2,1],[1,3]] 都是合法的。

示例 3：

1 <= pairs.length <= 105
pairs[i].length == 2
0 <= starti, endi <= 109
starti != endi
pairs 中不存在一模一样的数对。
至少存在一个合法的 pairs 重新排列。

class Solution {
public:
  vector<vector<int>> validArrangement(vector<vector<int>>& pairs) {
    map<int, vector<int>>g;
    for (auto& p : pairs)g[p[0]].push_back(p[1]);
    stack<int>s = Hierholzer(g.size(), g, 1, pairs[0][0]).euler;
    int a = s.top(), b;
    s.pop();
    vector<vector<int>>ans(s.size());
    for(int i=0;i<ans.size();i++) {
      b = s.top();
      ans[i] = vector<int>{ a, b };
      a = b;
      s.pop();
    }
    return ans;
  }
};

欧拉回路、链路

一，欧拉回路、欧拉链路

二，无向图

三，有向图

四，Hierholzer算法

1，递归版

力扣 332. 重新安排行程（有向图的欧拉链路）

力扣 753. 破解保险箱（有向图的欧拉回路）

2，非递归版

力扣 2097. 合法重新排列数对（有向图的欧拉回路或链路）

继续阅读

Codeforces 1417 D. Make Them Equal(思维+构造)

查找算法之二分查找查找算法之二分查找

查找算法学习之二分查找（Python版本）——BinarySearch

CQ V1.0分词bates(基于双数组tire树)—应该是目前最快的中文分词算法

Command Network(POJ 3164)---定根最小树形图模板题题目描述输入格式输出格式输入样例输出样例分析源程序

开源低带宽语音编解码器

241 Different Ways to Add Parentheses（C代码版）

【趋高机器视觉】机器视觉技术原理解析及解决方案

CSMA/CD1． CSMA/CD的概述2． CSMA 的工作原理3． CSMA/CD控制规程及特点4． CSMA/CD协议5． CSMA/CD的优点6．结束语

极大似然法(ML)与最大期望法(EM)

C++ 第十五周报告1--《冒泡法排序》

笔试面试题目：滑动窗口(二)

数据结构与算法（27）——排序（二）

Dijkstra--简易版（最短路径）

GitHub连夜封杀！这份阿里 10W 字内部 Java 字面试手册到底有多强？

hdu7108哈希