[leetcode]785. Is Graph Bipartite? [bai'pɑrtait] 判斷二分圖

Given an undirected 

graph

, return 

true

 if and only if it is bipartite.

Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation: 
The graph looks like this:
0----1
|    |
|    |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.

      

Example 2:
Input: [[1,2,3], [0,2], [0,1,3], [0,2]]
Output: false
Explanation: 
The graph looks like this:
0----1
| \  |
|  \ |
3----2
We cannot find a way to divide the set of nodes into two independent subsets.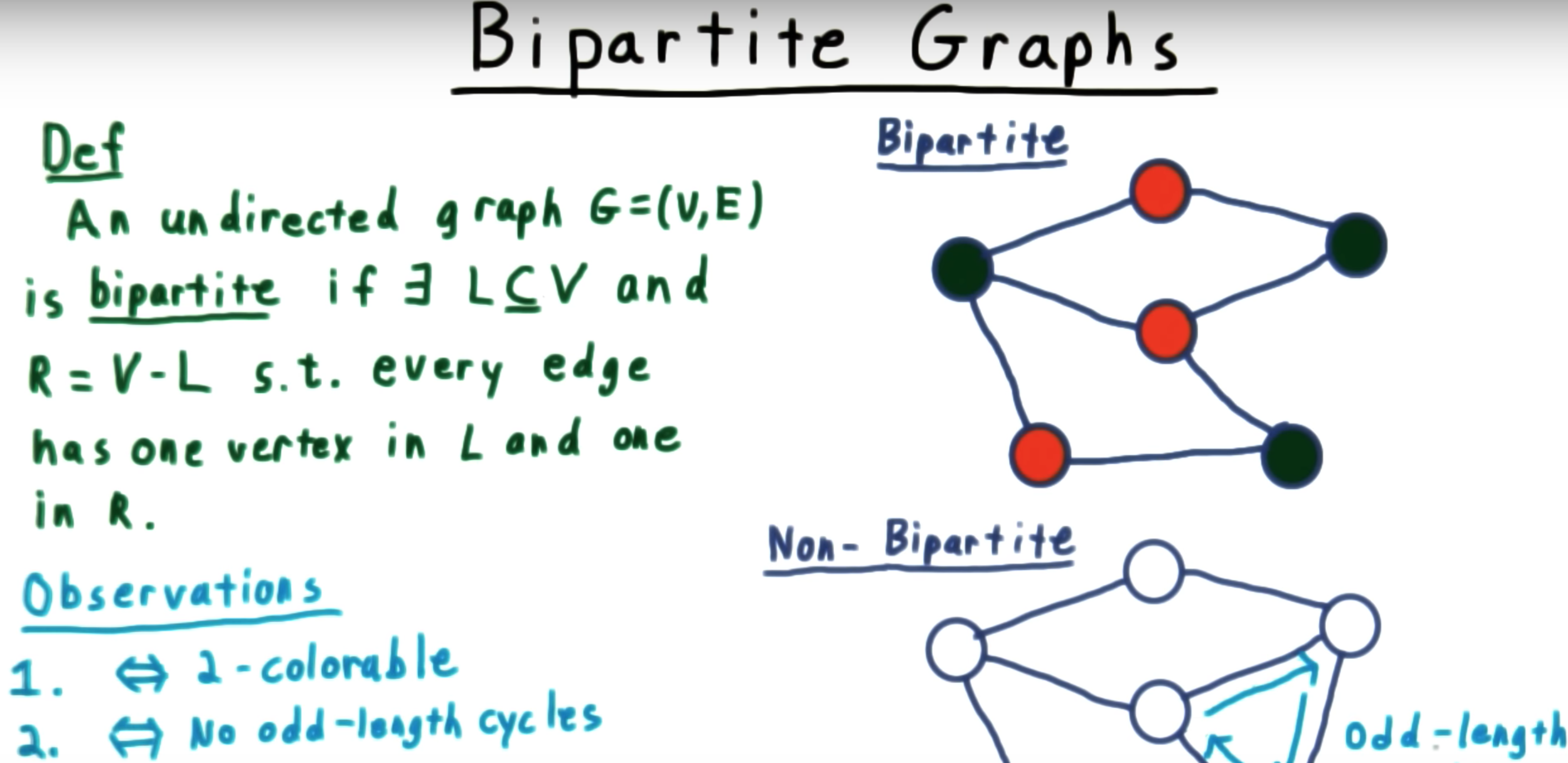      

設G=(V,E)是一個無向圖。如頂點集V可分割為兩個互不相交的子集V1,V2之并，并且圖中每條邊依附的兩個頂點都分别屬于這兩個不同的子集

思路

1. based on Graph Bipartite attribute, we can fill two different color for each subset.

2. if not Graph Bipartite, at lease one node such that its color happens to be the same as its neighbor

3. coz we need to traversal each node, we can both use dfs and bfs

代碼

1 class Solution {
 2     public boolean isBipartite(int[][] graph) {
 3         int[] visited = new int[graph.length];
 4         //default 0: not visited;
 5         //lable 1: green
 6         //lable 2: red     
 7         for(int i = 0; i < graph.length; i++) {
 8             // such node has been visited
 9             if(visited[i] != 0) {continue;}    
10             //such node has not been visited
11             Queue<Integer> queue = new LinkedList();
12             queue.add(i);
13             // mark as green
14             visited[i] = 1;
15             while(!queue.isEmpty()) {
16                 int cur = queue.poll();
17                 int curLable = visited[cur];
18                 // if curLable is green, fill neighborLable to red
19                 int neighborLable = curLable == 1? 2:1;
20                 for(int neighbor:graph[cur]) {
21                     //such node has not been visited
22                     if(visited[neighbor] == 0) {
23                         visited[neighbor] = neighborLable;
24                         queue.add(neighbor);
25                     }  
26                     // node visited, and visited[neighbor] != neighborLable, conflict happens
27                     else if(visited[neighbor] != neighborLable) {
28                         return false;
29                     }
30                 }
31             }       
32         }  
33         return true;
34     }
35 }      

轉載于:https://www.cnblogs.com/liuliu5151/p/9814350.html