第二十八講 R語言-Cox比例風險模型1
我該咋篩選變量進入多因素回歸?先教你基礎幾招! - 知乎 (zhihu.com)
(64條消息) 分類,等級,或者有序變量如何進行多因素Cox回歸 變量的類型決定了最終結果的reference_YoungLeelight的部落格-CSDN部落格
在第二十五到二十七講中,我們介紹了生存分析的基本概念,KM生存曲線及繪圖,以及比較多組生存曲線是否存在差異。KM生存曲線和Log-rank檢驗是單變量多分析方法,隻能通過分層的方式,考慮一個水準(因子/因素)的作用,而忽略其他因素多影響。但是當資料存在多個因素需要考慮,或因素不是分類變量,而是連續型變量時,KM曲線和Log-rank檢驗就無法應對了。這時,該怎麼辦呢?Cox比例風險模型應運而生。
Cox比例風險模型(proportional hazards model,簡稱Cox模型),是由英國統計學家D.R.Cox(1972) 年提出的一種半參數回歸模型。該模型以生存結局和生存時間為應變量,可同時分析衆多因素對生存期的影響,能分析帶有截尾生存時間的資料,且不要求估計資料的生存分布類型。
1. Cox比例風險模型的概念
在實際臨床研究中,影響事件發生的因素往往不止一個,它是多個因素綜合作用的結果。Cox比例風險模型,它既适用于連續型變量也适用于類别變量。此外,Cox回歸模型擴充了生存分析方法,以同時評估幾種風險因素對生存時間的影響,并且給每一個因素提供了統計量的大小以反映因素對事件發生的影響大小。
該模型的目的是同時評估多種因素對生存的影響。換句話說,它使我們可以探索特定因素是如何影響特定時間點的特定事件(例如,感染,死亡)發生率低。該比率通常稱為風險率。預測變量(或因子)在生存分析中通常稱為協變量(covariates)。
Cox模型由h(t)表示的危險函數表示。簡而言之,風險函數可以解釋為在時間t死亡的風險。可以估計如下:
h(t)=h0(t)×exp(b1x1+b2x2+...+bpxp)
其中,
- t表示生存時間
- h(t)是由一組數量為p的協變量 (x1,x2,...,xpx1,x2,...,xp)
- 系數 (b1,b2,...,bpb1,b2,...,bp)可以衡量協變量的影響(即影響大小)。
- h0被稱為基準風險,即當所有xi等于零(exp(0)數值等于1)時的事件風險。H(t)中的“t”表示該風險是随時間變化的。
Cox模型可以寫成多元線性模型的形式:
Ln(h(t))= (b1x1+b2x2+...+bpxp) + ln(h0(t))
Exp(bi)稱為風險比(Hazard ratios,HR)。值bi大于零,即風險比大于1,表示随着協變量ith的增加,事件風險也增加,于是生存期減少。
換句話說,風險比大于1表示協變量與事件機率正相關,與生存時間負相關 。
綜上所述,
- HR = 1:無效
- HR < 1:減少風險
- HR > 1:增加風險
請注意,在癌症研究中:
- 風險比 > 1(即:b > 0)的協變量稱為不良預後因素
- 風險比 < 1(即:b < 0)的協變量被稱為良好預後因素
Cox模型的一個關鍵假設條件是觀察組(或患者)的生存曲線應成比例,并且不能交叉。
比如,考慮兩個x值不同的患者k和k'。其相應的危險函數可以簡單地寫成如下
- 對患者k的風險函數:
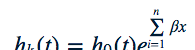
- 對患者k'的風險函數:
- 這兩名患者的危險比
應該要與時間t無關。
是以,Cox模型是比例風險模型:即在任何組中,事件的風險都是在協變量的影響下成比例變化的。是以,在Cox比例風險模型中,各組的生存曲線也應成比例,并且不能交叉。
換句話說,如果一個人在某個初始時間點的死亡風險是另一個人的兩倍,那麼在以後的所有時間,死亡風險仍然要是另一個人的兩倍。
我們将在第三十講中,為大家介紹,如何評估Cox比例風險模型的假設條件。
2. Cox比例風險模型的R實作
2.1安裝并加載所需的R包
我們将使用兩個R包:
- survival用于計算生存分析
- survminer用于總結和可視化生存分析結果
- 安裝軟體包
install.packages(c("survival", "survminer"))
- 加載軟體包
library("survival")
library("survminer")
2.2 用于計算Cox模型的R函數:coxph()
生存包中的函數coxph()可用于計算R中的Cox比例風險回歸模型。
簡化格式如下:
coxph(formula, data, method)
•formula:是将生存對象作為響應變量的線性模型。 使用功能Surv()建立生存對象:Surv(time,event)。
•data:包含變量的資料框
•method:用于指定如何處理領帶。 預設值為“efron”。 其他選項是“breslow”和“exact”。 通常,預設的“efron”優于曾經流行的“breslow”方法。 “exact”方法的計算量會很大。
2.3 示例資料集
我們将使用survival包中提供的肺癌資料。
data("lung")
head(lung)
inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1 3 306 2 74 1 1 90 100 1175 NA
2 3 455 2 68 1 0 90 90 1225 15
3 3 1010 1 56 1 0 90 90 NA 15
4 5 210 2 57 1 1 90 60 1150 11
5 1 883 2 60 1 0 100 90 NA 0
6 12 1022 1 74 1 1 50 80 513 0
- inst:機構代碼
- time:以天為機關的生存時間
- status:删失狀态1 = 删失,2 = 出現失效事件
- age:歲
- sex:性别,男= 1女= 2
- ph.ecog:ECOG評分(0 =好,5 =死)
- ph.karno:醫師進行的Karnofsky評分(0 = 差,100 = 好)
- pat.karno:患者自行進行的Karnofsky評分(0 = 差,100 = 好)
- meal.cal:用餐時消耗的卡路裡
- wt.loss:最近六個月的體重減輕
2.4 計算Cox模型
我們将使用以下協變量來拟合Cox回歸:age,sex,ph.ecog和wt.loss。
我們首先計算所有這些變量的單變量Cox分析。然後我們将使用兩個變量來拟合多變量Cox分析,以描述這些因素如何共同影響生存。
2.4.1 單變量Cox模型
單變量Cox分析可以如下計算:
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
res.cox
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
coef exp(coef) se(coef) z p
sex -0.531 0.588 0.167 -3.18 0.0015
Likelihood ratio test=10.6 on 1 df, p=0.00111
n= 228, number of events= 165
Cox模型的功能summary()産生更完整的報告:
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
n= 228, number of events= 165
coef exp(coef) se(coef) z Pr(>|z|)
sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.588 1.701 0.4237 0.816
Concordance= 0.579 (se = 0.022 )
Rsquare= 0.046 (max possible= 0.999 )
Likelihood ratio test= 10.63 on 1 df, p=0.001111
Wald test = 10.09 on 1 df, p=0.001491
Score (logrank) test = 10.33 on 1 df, p=0.001312
Cox回歸結果可以解釋為:
- 統計意義:标記為“z”的列給出了Wald的統計量。它對應于每個回歸系數與其标準誤的比率(z = coef / se(coef))。Wald統計量會評估beta(β,coef)給定變量的系數在統計上是否與0有顯著差異。從上面的輸出中,我們可以得出結論,變量sex的系數(coef)與0具有統計學差異(P = 0.00149)。
- 回歸系數。Cox模型結果中要注意的第二個特征是回歸系數(coef)的符号。正号表示該變量值為不良風險因素,與受試者高事件發生率有關,是以預後較差。變量sex被編碼為數字向量。1:男性; 2:女性。Cox模型的summary()提供了第二組相對于第一組(即女性與男性)的風險比(HR,exp(coef))。在這些資料中,性别的β系數(coef)= -0.53,表示女性比男性具有更低的死亡風險。
- 風險比。指數系數(exp(coef)= exp(-0.53)= 0.59),也稱為風險比,給出了協變量的影響大小。例如,女性(性别= 2)可将危險降低0.59或41%。女性是良好預後的因素。
- 風險比的置信區間。Summary()輸出還給出了風險比(exp(coef))的 95%置信區間,下限95%= 0.4237,上限95%= 0.816。
- 模型的全局統計意義。最後,結果中輸出了模型的總體重要性檢驗結果,病提供了三個備選檢驗的p值:似然比檢驗(likelihood-ratio test),Wald檢驗(Wald test)和得分對數秩統計(score logrank statistics)。這三種方法基本等效。對于足夠大的N,它們将給出相似的結果。對于較小的N,它們可能會有所不同。對于小樣本量,似然比檢驗結果更準确,是以通常是首選。
要将單變量coxph函數一次應用于多個協變量,請輸入以下指令:
covariates <- c("age", "sex", "ph.karno", "ph.ecog", "wt.loss")
univ_formulas <- sapply(covariates,
function(x) as.formula(paste('Surv(time, status)~', x)))
univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)})
# 提取資料,并制作資料表格
univ_results <- lapply(univ_models,
function(x){
x <- summary(x)
p.value<-signif(x$wald["pvalue"], digits=2)
wald.test<-signif(x$wald["test"], digits=2)
beta<-signif(x$coef[1], digits=2);#coeficient beta
HR <-signif(x$coef[2], digits=2);#exp(beta)
HR.confint.lower <- signif(x$conf.int[,"lower .95"], 2)
HR.confint.upper <- signif(x$conf.int[,"upper .95"],2)
HR <- paste0(HR, " (",
HR.confint.lower, "-", HR.confint.upper, ")")
res<-c(beta, HR, wald.test, p.value)
names(res)<-c("beta", "HR (95% CI for HR)", "wald.test",
"p.value")
return(res)
#return(exp(cbind(coef(x),confint(x))))
})
res <- t(as.data.frame(univ_results, check.names = FALSE))
as.data.frame(res)
beta HR (95% CI for HR) wald.test p.value
age 0.019 1 (1-1) 4.1 0.042
sex -0.53 0.59 (0.42-0.82) 10 0.0015
ph.karno -0.016 0.98 (0.97-1) 7.9 0.005
ph.ecog 0.48 1.6 (1.3-2) 18 2.7e-05
wt.loss 0.0013 1 (0.99-1) 0.05 0.83
上面的輸出顯示了每個變量相對于總生存率的回歸beta系數,效應大小(以風險比給出)和統計顯着性。通過單獨的單變量Cox回歸評估每個因素。
從上面的輸出中,
- 性别,年齡和ph.ecog變量具有極高的統計學意義,而ph.karno的系數則不顯着。
- 年齡和ph.ecog具有正β系數,而性别具有負系數。是以,年齡較大和phogog較高與事件發生率呈正相關,而女性(性别= 2)則與事件發生率呈負相關。即年齡和phogog是死亡的危險因素,女性性别是死亡的保護因素。
現在,我們要描述這些因素如何共同影響生存。為了回答這個問題,我們将執行多元Cox回歸分析。由于變量ph.karno在單變量Cox分析中不重要,是以在多變量分析中将其跳過。我們将3個因素(性别,年齡和ph.ecog)納入多元模型。
下一講中, 我們将介紹,在經過單變量Cox分析後選取的多個因素,如何進行多元Cox回歸分析,如何解釋回歸分析的結果,以及如何通過作圖來展示結果。
2.4.2 多元Cox回歸分析
多元cox回歸分析的R代碼如下,其中3個因素(性别,年齡和ph.ecog)納入多元模型:
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
n= 227, number of events= 164
(1 observation deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
age 0.011067 1.011128 0.009267 1.194 0.232416
sex -0.552612 0.575445 0.167739 -3.294 0.000986 ***
ph.ecog 0.463728 1.589991 0.113577 4.083 4.45e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
exp(coef) exp(-coef) lower .95 upper .95
age 1.0111 0.9890 0.9929 1.0297
sex 0.5754 1.7378 0.4142 0.7994
ph.ecog 1.5900 0.6289 1.2727 1.9864
Concordance= 0.637 (se = 0.026 )
Rsquare= 0.126 (max possible= 0.999 )
Likelihood ratio test= 30.5 on 3 df, p=1.083e-06
Wald test = 29.93 on 3 df, p=1.428e-06
Score (logrank) test = 30.5 on 3 df, p=1.083e-06
所有三個總體檢驗(似然性,Wald和得分)的p值均顯着,表明該模型具有顯着性意義。這些檢驗評估了總體beta的綜合原假設(β)為0。在上面的示例中,檢驗統計資料非常一緻,并且完全拒絕了綜合原假設。即由3個因素(性别,年齡和ph.ecog)組成的模型對風險比的影響系數不為0。
在元Cox分析中,協變量性别和ph.ecog保持顯着性(p <0.05)。但是,協變量年齡不顯着(p = 0.23,大于0.05)。
性别的p值為0.000986,風險比HR = exp(coef)= 0.58,表明患者的性别與死亡風險降低之間有很強的關系。協變量的風險比可解釋為對危險的倍增效應。例如,保持其他協變量不變的前提條件下,女性(性别= 2)相比于男性,死亡風險低0.58或42%。我們得出的結論是,成為女性與良好的預後相關。
同樣,ph.ecog的p值為4.45e-05,風險比HR = 1.59,表明ph.ecog值與死亡風險增加之間有很強的關系。如果保持其他協變量不變,則ph.ecog的值越高,存活率越低,即在其他協變量都一緻的人群中,ph.ecog每增高一個機關,死亡風險增高59%。
相比之下,年齡的p值現在為p = 0.23。風險比HR = exp(coef)= 1.01,95%置信區間為0.99至1.03。由于HR的置信區間為1,是以該結果表明,在調整了ph.ecog值和患者的性别後,年齡對HR差異的貢獻較小,并且不顯着。例如,在其他協變量保持不變的情況下,每老一歲會引起每日死亡危險, 1%,但這并沒有統計學意義,也不是重大貢獻。
3. 可視化生存時間的估計分布情況
将Cox模型拟合到資料後,就可以可視化特定風險組在任何給定時間點的預測的生存率。函數survfit()估計生存比例,預設情況下輸出的為協變量的平均值。
與KM生存曲線不同的是,Cox模型拟合曲線輸出的是在矯正了其他協變量因素以後的預測的生存率,而不是實際觀察到的生存率情況。
# 繪出基線的生存函數
ggsurvplot(survfit(res.cox), color = "#2E9FDF",
ggtheme = theme_minimal())
我們可能希望顯示估算的生存率如何被特定協變量影響的。
考慮到這一點,我們想評估性别對估計生存率的影響。在這種情況下,我們先建立一個有兩行的新資料表,每一行代表一種性别。其他協變量則固定為其平均值(如果是連續變量)或最低水準(如果它們是離散變量)。對于協變量為啞變量的,平均值為資料集中編碼為1的比例。該資料表通過newdata參數傳遞給survfit():
# 建立新的資料表
sex_df <- with(lung,
data.frame(sex = c(1, 2),
age = rep(mean(age, na.rm = TRUE), 2),
ph.ecog = c(1, 1)
)
)
sex_df
sex age ph.ecog
1 1 62.44737 1
2 2 62.44737 1
# 繪制曲線圖
fit <- survfit(res.cox, newdata = sex_df)
ggsurvplot(fit, conf.int = TRUE, legend.labs=c("Sex=1", "Sex=2"),
ggtheme = theme_minimal())
參考内容:http://www.sthda.com