十大排序6--歸并排序(MergetSort)

歸并排序

歸并排序,利用歸并的思想實作排序,該方法才采用經典的分治政策,成一些小的問題然後遞歸求解， 而治的階段則将分的階段得到各答案"修補"在一起即分而治之

歸并排序思想示意圖 1-基本思想:

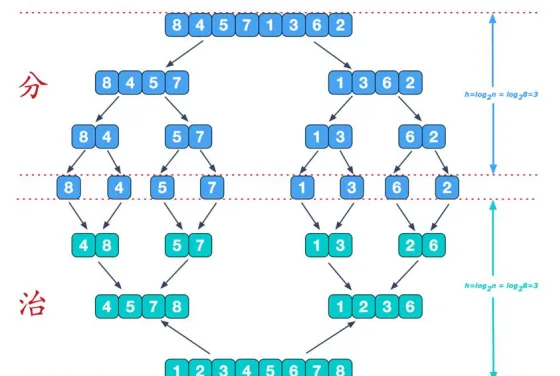
歸并排序思想示意圖 2-合并相鄰有序子序列:

取中間的值作為基準,兩邊的進行合并.類似于連結清單合并

package com.nie.sort;

import java.util.Arrays;

/*
歸并排序
 */
public class MergetSort {

    public static void main(String[] args) {
        int arr[] = {8, 4, 5, 7, 1, 3, 6, 2};
        int temp[] = new int[arr.length];
        mergeSort(arr, 0, arr.length - 1, temp);
        System.out.println(Arrays.toString(arr));
    }
    //分+合
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if (left < right) {
            //中間索引
            int mid = (left + right) / 2;
            //向左遞歸進行分解
            mergeSort(arr, left, mid, temp);
            //向右遞歸進行分解
            mergeSort(arr, mid + 1, right, temp);
            //合并
            merge(arr, left, mid, right, temp);
        }
    }

    /**
     * @param arr   排序的原始數組
     * @param left  左邊有序序列的初始索引
     * @param mid   中間索引
     * @param right 右邊索引
     * @param temp  作為中轉的數組
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        int i = left;
        int j = mid + 1;
        int t = 0;

        //(一)
        //先把左右兩邊(有序)的資料按照規則填充到temp數組
        //直到左右兩邊的有序序列，有一邊處理完畢為止
        while (i <= mid && j <= right) {
            //如果左邊的有序序列的目前元素，小于等于右邊有序序列的目前元素
            //即将左邊的目前元素，填充到 temp數組
            //然後 t++, i++
            if (arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t++;
                i++;
            } else {//反之,将右邊有序序列的目前元素，填充到temp數組
                temp[t] = arr[j];
                t++;
                j++;
            }

        }
        //(二)
        //把有剩餘資料的一邊的資料依次全部填充到temp
        while (i <= mid) {//左邊的有序序列還有剩餘的元素，就全部填充到temp
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }
        while (j <= right) {//右邊的有序序列還有剩餘的元素，就全部填充到temp
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }
        //(三)
        //将temp數組的元素拷貝到arr
        //注意，并不是每次都拷貝所有
        t = 0;
        int tempLeft = left;
        //第一次合并 tempLeft = 0 , right = 1 //  tempLeft = 2  right = 3 // tL=0 ri=3
        //最後一次 tempLeft = 0  right = 7
        while (tempLeft <= right) {
            arr[tempLeft] = temp[t];
            t += 1;
            tempLeft++;
        }
    }
}      

hh      

總結:

平均時間複雜度O(nlogn)

最好情況 O(nlog n)

最壞情況 O(nlog n)

空間複雜度 O(n)