在我們做統計分析之前,面對大量雜亂無章的數字往往會做個散點圖,以對資料有直覺的了解。例如,某超市的銷售主管想要知道,顧客的收入水準是否對購買新的智能手機有影響。為此,他選擇了12為顧客,調查他們的月收入(X)以及是否購買了新的手機,購買記為{Y=1},未購買記為{Y=0}。調查結果為12位受訪者有7位購買了新手機。
我們的第一想法就是試試用線性回歸看能否較好地描述這個問題。
是以可得以下回歸直線:P=-0.749+0.0003358*X。這裡的Y值可表示為購買手機的機率,但是這裡出現了兩個問題:一是當收入很小時,P值可為負,當收入很大時,P值會大于1;二是當購買機率接近于1或0時,機率對自變量(收入水準)的變化就不是很敏感,即這附近,收入需要很大的變化,才能引起機率P的變化(系數很小)。既然如此,我們如何去修正呢?我們就需要引入logit變換的概念。
Logistic變換Logistic回歸不是估計二進制因變量的觀察值,而是要推導出這些觀察值出現的機率。為了能确定事件Y發生的機率,我們假設存在一個關于機率p的函數Ɵ=f(p),此函數形式簡單,且為單調函數。根據數學中導數的定義,以f'(p)反映在p附近的變化,同時,在p=0或1附近時,f'(p)有較大的值,于是取函數f'(p)(公式1),即f(p)(公式2),稱此式為Logistic變換。
可以看出當f'(p)>0時,Ɵ=f(p)為p的增函數,且當p從0至1變化時,Ɵ在(-∞,+∞)上變化,這一變換也解決了上述出現的兩個問題,在資料處理上也帶來了很多友善。
為了建立因變量P與自變量X之間的合理的變化關系,我們令
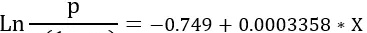
經過換算,則顧客手機購買機率:
一般的,Y 是0,1變量,X是任意k個變量,那麼變量Y關于變量X的k元logistic回歸模型為公式3,其中,對于二值變量Y關于變量X的一進制logistic回歸模型即公式4:
其中α和β是未知參數或待估計的回歸系數,該模型描述了y取某個值(這裡y=1)的機率P與自變量X之間的關系。
小結:本期,我們從一個小的案例出發,逐漸分析,利用數學知識描述了從簡單線性回歸到logistic回歸的過程,下期我們将簡要介紹logistic回歸系數的相關問題,以期對模型有更深的認識。
關于Logistic回歸概述,小夥伴們可以回顧本系列的第一篇推文《Logistic回歸系列(一)——Logistic回歸概述》。
本期參考:
- 《Logistic回歸入門》[美]Fred C. Pampel著,周穆之譯,陳偉校;
- 《Logistic回歸模型分析綜述及應用研究》 [碩士論文] 尹建傑,黑龍江大學 ,2011