批量歸一化
訓練深層神經網絡是十分困難的,特别是在較短的時間内使他們收斂更加棘手。 批量歸一化(batch normalization)這是一種流行且有效的技術,可持續加速深層網絡的收斂速度。 批量歸一化使得我們能夠訓練 100 層以上的網絡。
1 訓練深層網絡
首先,資料預處理的方式通常會對最終結果産生巨大影響。使用真實資料時,我們的
第一步是标準化輸入特征,使其平均值為0,方差為1。這種标準化可以很好地與我們的優化器配合使用,因為它可以将參數的量級進行統一。
第二,對于典型的多層感覺機或卷積神經網絡。當我們訓練時,中間層中的變量(例如,多層感覺機中的仿射變換輸出)可能具有更廣的變化範圍:不論是沿着從輸入到輸出的層,跨同一層中的單元,或是随着時間的推移,模型參數的随着訓練更新變幻莫測。 批量歸一化的發明者非正式地假設,這些變量分布中的這種偏移可能會阻礙網絡的收斂。 直覺地說,我們可能會猜想,如果一個層的可變值是另一層的 100 倍,這可能需要對學習率進行補償調整。
第三,更深層的網絡很複雜,容易過拟合。 這意味着正則化變得更加重要。
批量歸一化應用于單個可選層(也可以應用到所有層),其原理如下:在每次訓練疊代中,我們首先歸一化輸入,即通過減去其均值并除以其标準差,其中兩者均基于目前小批量處理。 接下來,我們應用比例系數和比例偏移。 正是由于這個基于批量統計的标準化,才有了批量歸一化的名稱。
請注意,如果我們嘗試使用大小為 1 的小批量應用批量歸一化,我們将無法學到任何東西。 這是因為在減去均值之後,每個隐藏單元将為 0。 是以,隻有使用足夠大的小批量,批量歸一化這種方法才是有效且穩定的。 請注意,在應用批量歸一化時,批量大小的選擇可能比沒有批量歸一化時更重要
正向傳播是從資料到損失函數,反向傳播是從損失函數到資料,反向傳播的時候剛開始梯隊可能很大,但是随着反向傳播要乘以記錄的梯度(偏導)就會越來越小。是以越靠近損失函數收斂的就越快
越靠近資料收斂的越慢。這樣導緻的問題是每次底層(資料)訓練完上層(損失函數)就要拟合資料
就會導緻收斂比較慢。這裡引出了一個問題,我們可以在學習底部層(資料層)的時候能不能避免變化頂部層(損失函數)
量歸一化 BN 根據以下表達式轉換 x
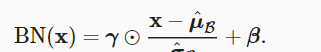
另外,批量歸一化圖層在”訓練模式“(通過小批量統計資料歸一化)和“預測模式”(通過資料集統計歸一化)中的功能不同。 在訓練過程中,我們無法得知使用整個資料集來估計平均值和方差,是以隻能根據每個小批次的平均值和方差不斷訓練模型。 而在預測模式下,可以根據整個資料集精确計算批量歸一化所需的平均值和方差。
對于全連接配接層行為樣本每一列為特征
對于卷積層每一個像素可以看成一個樣本,樣本數可以看成批量大小高寬那麼對于每一個像素樣本對應的特征數就是它所對應的通道數所對應位置的像素
批量歸一化加速收斂但不改變模型精度
2 代碼
import torch
from torch import nn
from d2l import torch as d2l
#X層的輸入, gamma和beta需要學習的參數 moving_mean全局均值 moving_var全集方差(可以了解為整個資料集上的均值和方差)
#momentum(取固定數字)用來更新moving_mean和moving_var eps表示批量歸一化裡面的那個一不西諾
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通過 `is_grad_enabled` 來判斷目前模式是訓練模式還是預測模式
if not torch.is_grad_enabled():
# 如果是在預測模式下,直接使用傳入的移動平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)#2代表全連接配接層,4代表卷積層
if len(X.shape) == 2:
# 使用全連接配接層的情況,計算特征維上的均值和方差
mean = X.mean(dim=0) #按行求均值,也就是說對每一列算一個均值
var = ((X - mean) ** 2).mean(dim=0)#按行求方差,也就是說對每一列算一個方差
else: #2D卷積的情況
# 使用二維卷積層的情況,計算通道維上(axis=1)的均值和方差。
# 這裡我們需要保持X的形狀以便後面可以做廣播運算
mean = X.mean(dim=(0, 2, 3), keepdim=True) #沿着通道維求均值
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)#沿着通道維求方差
# 訓練模式下,用目前的均值和方差做标準化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移動平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 縮放和移位
return Y, moving_mean.data, moving_var.data
#建立一個BatchNorm圖層
class BatchNorm(nn.Module):
# `num_features`:完全連接配接層的輸出數量或卷積層的輸出通道數。
# `num_dims`:2表示完全連接配接層,4表示卷積層
def __init__(self, num_features, num_dims): #num_dims這個值是一個網絡型号的代号? 啊這是次元!!
super().__init__()
if num_dims == 2: #如果是全連接配接網絡
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 參與求梯度和疊代的拉伸和偏移參數,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape)) #需要被疊代
self.beta = nn.Parameter(torch.zeros(shape))#需要被疊代
# 非模型參數的變量初始化為0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果 `X` 不在記憶體上,将 `moving_mean` 和 `moving_var`
# 複制到 `X` 所在顯存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device) #放到GPU上
self.moving_var = self.moving_var.to(X.device) #放到GPU上
# 儲存更新過的 `moving_mean` 和 `moving_var`
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean,
self.moving_var, eps=1e-5, momentum=0.9)
return Y
#使用批量歸一化層的 LeNet模型
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
nn.Linear(84, 10))
#訓練
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()
總結
提示:這裡對文章進行總結:
例如:以上就是今天要講的内容,本文僅僅簡單介紹了pandas的使用,而pandas提供了大量能使我們快速便捷地處理資料的函數和方法。