題目描述
這是 LeetCode 上的 417. 太平洋大西洋水流問題 ，難度為 中等。
Tag : 「DFS」、「BFS」、「多源 BFS」
有一個
m × n
的矩形島嶼，與 太平洋 和 大西洋 相鄰。 “太平洋” 處于大陸的左邊界和上邊界，而 “大西洋” 處于大陸的右邊界和下邊界。
這個島被分割成一個由若幹方形單元格組成的網格。給定一個
m x n
的整數矩陣
heights
， 表示坐标 上單元格 高于海平面的高度 。
島上雨水較多，如果相鄰單元格的高度 小于或等于 目前單元格的高度，雨水可以直接向北、南、東、西流向相鄰單元格。水可以從海洋附近的任何單元格流入海洋。
傳回 網格坐标
result
的 2D清單 ，其中 表示雨水可以從單元格 流向 太平洋和大西洋 。
示例 1：
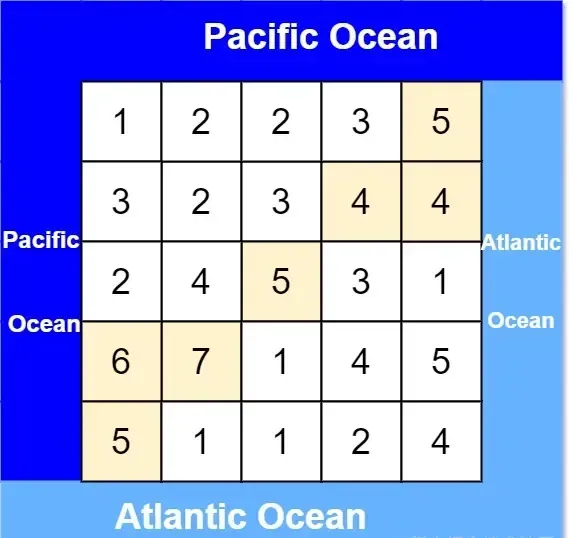
輸入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
輸出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]] 示例 2：
輸入: heights = [[2,1],[1,2]]
輸出: [[0,0],[0,1],[1,0],[1,1]] 提示：
基本分析
整理題意，需要我們統計能夠同時流向兩片海域的格子。
從源點（格子）流向彙點（海域）是按照高度從高到低（非嚴格）的規則，那麼反過來從海域到格子則是按照從低到高（非嚴格）規則進行，同時本身處于邊緣的格子與海域聯通。
是以我們可以使用兩遍
DFS/BFS
進行求解：分别從與目前海域直接相連的邊緣格子出發，統計能夠流向目前海域的格子集合，兩片海域求得的集合交集即是答案。
BFS（多源 BFS）
使用
BFS
進行求解：目的是構造出兩個答案矩陣 和 ， 代表格子 能夠流向海域，起始将所有與海域相連的格子放入隊列，然後跑一遍
BFS
，所有能夠進入隊列的格子均能夠與海域聯通。
最後統計所有滿足 的格子即是答案。
代碼：
class Solution {
int n, m;
int[][] g;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
g = heights;
m = g.length; n = g[0].length;
Deque<int[]> d1 = new ArrayDeque<>(), d2 = new ArrayDeque<>();
boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
res1[i][j] = true;
d1.addLast(new int[]{i, j});
}
if (i == m - 1 || j == n - 1) {
res2[i][j] = true;
d2.addLast(new int[]{i, j});
}
}
}
bfs(d1, res1); bfs(d2, res2);
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (res1[i][j] && res2[i][j]) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void bfs(Deque<int[]> d, boolean[][] res) {
while (!d.isEmpty()) {
int[] info = d.pollFirst();
int x = info[0], y = info[1], t = g[x][y];
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (res[nx][ny] || g[nx][ny] < t) continue;
d.addLast(new int[]{nx, ny});
res[nx][ny] = true;
}
}
}
} - 時間複雜度：
BFS
- 空間複雜度：
DFS
同理，使用
DFS
進行求解。
代碼：
class Solution {
int n, m;
int[][] g;
public List<List<Integer>> pacificAtlantic(int[][] heights) {
g = heights;
m = g.length; n = g[0].length;
boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 || j == 0) {
if (!res1[i][j]) dfs(i, j, res1);
}
if (i == m - 1 || j == n - 1) {
if (!res2[i][j]) dfs(i, j, res2);
}
}
}
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (res1[i][j] && res2[i][j]) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void dfs(int x, int y, boolean[][] res) {
res[x][y] = true;
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (res[nx][ny] || g[nx][ny] < g[x][y]) continue;
dfs(nx, ny, res);
}
}
} - 時間複雜度：
DFS
- 空間複雜度：
并查集
其中維護連通性部分可以使用「并查集」來做：起始将與海域 A 聯通的邊緣格子與
S
聯通，将與海域 B 聯通的邊緣格子與
T
聯通，然後跑一遍
DFS/BFS
，最後将既和
S
聯通又和
T
聯通的格子加入答案。
代碼：
class Solution {
int N = 200 * 200 + 10;
int[] p1 = new int[N], p2 = new int[N];
int n, m, tot, S, T;
int[][] g;
void union(int[] p, int a, int b) {
p[find(p, a)] = p[find(p, b)];
}
int find(int[] p, int x) {
if (p[x] != x) p[x] = find(p, p[x]);
return p[x];
}
boolean query(int[] p, int a, int b) {
return find(p, a) == find(p, b);
}
int getIdx(int x, int y) {
return x * n + y;
}
public List<List<Integer>> pacificAtlantic(int[][] _g) {
g = _g;
m = g.length; n = g[0].length; tot = m * n; S = tot + 1; T = tot + 2;
for (int i = 0; i <= T; i++) p1[i] = p2[i] = i;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int idx = getIdx(i, j);
if (i == 0 || j == 0) {
if (!query(p1, S, idx)) dfs(p1, S, i, j);
}
if (i == m - 1 || j == n - 1) {
if (!query(p2, T, idx)) dfs(p2, T, i, j);
}
}
}
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int idx = getIdx(i, j);
if (query(p1, S, idx) && query(p2, T, idx)) {
List<Integer> list = new ArrayList<>();
list.add(i); list.add(j);
ans.add(list);
}
}
}
return ans;
}
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
void dfs(int[] p, int ori, int x, int y) {
union(p, ori, getIdx(x, y));
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if (query(p, ori, getIdx(nx, ny)) || g[nx][ny] < g[x][y]) continue;
dfs(p, ori, nx, ny);
}
}
} - 時間複雜度：
- 空間複雜度：
最後
這是我們「刷穿 LeetCode」系列文章的第
No.417
篇，系列開始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道題目，部分是有鎖題，我們将先把所有不帶鎖的題目刷完。
![Java String.format方法的簡單使用[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)