需求場景：抽獎送積分，積分範圍100-10000，要求平均1000積分。
這是一個很常見的需求，但是很難下手，一般人的解決方案都是先随機幾個數值判斷或者第一次随機一個小的第二次随機一個大的。
其實如果把需求轉換成數學函數你就會豁然開朗：
給定離散函數y=f(x)(x∈[100,10000],y>=0,)，使得y的期望值為1000。
但，這種函數千千萬，鬼知道是哪個...
正所謂弱水三千我們隻需一瓢，我們又不是來解數學題的，隻要找到一個符合條件的不就行了。
首先這個函數必須是曲線，是以我們就取最簡單的曲線y=ax²和y=1/ax。
部落客身先士卒，試過了y=ax²并不行，是以此處選擇y=1/ax的雙曲線。
還是那句話弱水三千我們隻需一瓢，越簡單越好是以直接指定a=1，為了更友善計算，我們再指定x=1時y=0，這樣就選好了一個雙曲線y=1/x-1。然後根據數學函數的特性，我們隻需要找到區間[m,1]，最大值f(m)，最小值0，平均值是1000/(10000-100)*f(m)（就是y值的0.1010101倍）就可以解決随機的問題了。
定積分肯定少不了了：
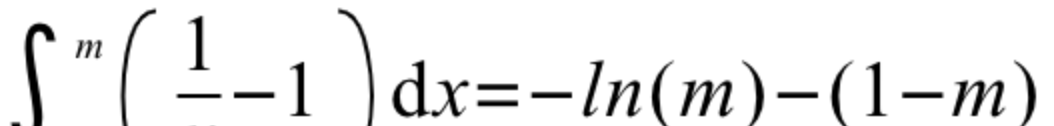
x=1時y=0是以平均值就是：dx/(1-m)
回回神，整個邏輯梳理一下，最終的結果就是：(-ln(m)-(1-m))/(1-m)=平均值，平均值=0.1010101*(1/m-1)，求m的值。
雖然已經簡化這麼多，但部落客反正是求不出來這個m的值😂。
仍然是那句話我們又不是來解數學題的，既然解不出來，作為程式猿怎麼能忘記初心呢：我們隻需要用代碼遞歸找到一個m使得平均值比例最趨近0.101010101不就行了。
函數y=1/x-1在(0,1)區間内是單調減的，是以直接采用二分法，然後遞歸調用。結合代碼的特性：double值是有限的，是以隻需要二分法後的值等于二分法左值、二分法右值、平均值中的一個就可以結束了。
此處需要注意的是y=1/x-1的平均值和最大值的比例隻會小于0.5，舉例就是：最小值100，最大值10000，則這個曲線最大隻能生成平均值為5049.99999（小于(10000-100)/2+100）的值。那我想要：最小值100，最大值10000，平均值9000的該如何解決？
拿10000-随機值不就是了😂
前面的你可以看不懂，但代碼會運作吧，不多啰嗦了，上代碼：
public static void main(String[] args) {
int min = 100;
int max = 10000;
int average = 1000;
System.out.println(start(min, max, average));
}
/**
* 開始計算區間
*
* @param min 最小随機數
* @param max 最大随機數
* @param average 平均值
* @return 傳回雙曲函數的左區間的值
*/
public static double start(double min, double max, double average) {
double targetRatio = (average - min) / (max - min);
System.out.println("-------------計算開始,最小值：" + min + "，最大值：" + max + "，平均值：" + average + "，目标比例：" + targetRatio + "---------------");
if (targetRatio >= 1 || targetRatio <= 0) {
throw new RuntimeException("你傻嗎");
}
if (targetRatio > 0.5d) {
double m = recursiveLeftInterval(0d, 1d, 1 - targetRatio);
System.out.println("\n\n-------------計算結果---------------");
System.out.println("函數y=" + max + "-(1/x-1)*(+" + max + "-" + min + ")/(1/" + m + "-1)" + "在區間[" + m + ",1]的平均值約：" + average);
return m;
} else if (targetRatio < 0.5d) {
double m = recursiveLeftInterval(0d, 1d, targetRatio);
System.out.println("\n\n-------------計算結果---------------");
System.out.println("函數y=(1/x-1)*(+" + max + "-" + min + ")/(1/" + m + "-1)+" + min + "在區間[" + m + ",1]的平均值約：" + average);
return m;
} else {
throw new RuntimeException("騷年國小數學不及格啊");
}
}
/**
* 請使用上面的start方法
* <p>
* 遞歸求y=1/x-1在區間[m,1]中m的值
*
* @param minM m的最小值,第一次傳0
* @param maxM m的最大值,第一次傳1
* @param targetRatio 目标比例必須<0.5,如果>0.5請反置
* @return 傳回左區間m的值
*/
private static double recursiveLeftInterval(double minM, double maxM, double targetRatio) {
//二分法m
double currentM = (maxM + minM) / 2;
//就是dx/(1-m)/(1/m-1)，簡化了一下，dx=-ln(m)-(1-m)
double currentRatio = currentM / (currentM - 1) / (currentM - 1) * (currentM - 1 - Math.log(currentM));
System.out.println("目前m的範圍[" + minM + "," + maxM + "]，目前m的值" + currentM + "]，目前比例" + currentRatio);
//精度上限
if (currentM == minM || currentM == maxM) {
System.out.println("達到double精度上限，最終m的範圍[" + minM + "," + maxM + "]，最終m的值" + currentM);
return currentM;
}
if (currentRatio > targetRatio) {//在範圍左邊
return recursiveLeftInterval(minM, currentM, targetRatio);
} else if (currentRatio < targetRatio) {//在範圍右邊
return recursiveLeftInterval(currentM, maxM, targetRatio);
}
System.out.println("計算比例剛好相等，最終m的範圍[" + minM + "," + maxM + "]，最終m的值：" + currentM);
return currentM;
}
列印的最終結果：0.03569086434475005
也許你啥都沒看懂，沒關系，隻要你能把上面的代碼改成自己的最大值、最小值、平均值然後跑起來，得到m，任務就完成了😂
至此你可以把上面的代碼都删掉了😂😂😂😂😂😂😂😂
真正使用：
/**
* 真正的使用是這樣的
*/
public static void example() {
System.out.println("\n\n-------------舉例最少50積分，最大5000積分，平均800積分---------------");
int min = 50;
int max = 5000;
int average = 800;
// double m= start(min,max,average);//大錯特錯，每次都計算多浪費性能
//m是寫死的，隻需要算過一次儲存下來就行了（若三個值有變動記得再算一遍）
double m = 0.07977647130071558;
double ratio = ((double) average - min) / (max - min);
//随機m~1的數
double random = Math.random() * (1d - m) + m;
//+0.5表示四舍五入
int integral;
//這裡的if是為了防止一些人比較笨，無腦複制導緻公式用錯
if (ratio > 0.5) {
//最小值100，最大值10000，平均值9000就會>0.5了。此時隻需要拿最大值減去随機值就行了
integral = (int) (max - (1 / random - 1) * (max - min) / (1 / m - 1) + 0.5);
} else {
//雙曲線的平均值都是<0.5的
integral = (int) ((1 / random - 1) * (max - min) / (1 / m - 1) + min + 0.5);
}
System.out.println("随機的一個積分" + integral);
// 随機驗證
System.out.println("\n\n-------------随機驗證統計區---------------");
//驗證循環次數
int totalCount = 1000000;
//積分總和
double sum = 0;
//統計随機出來的最大、最小積分
int statisticalMax = 0, statisticalMin = Integer.MAX_VALUE;
//統計每1/10的分布情況
int[] statisticalDistributions = new int[11];//max也要占一個坑，是以是11，第11個就是max的數量
for (int i = 0; i < totalCount; i++) {
//随機m~1之間的數
double random2 = Math.random() * (1 - m) + m;
//+0.5表示四舍五入
int integral2;
if (ratio > 0.5) {
integral2 = (int) (max - (1 / random2 - 1) * (max - min) / (1 / m - 1) + 0.5);
} else {
integral2 = (int) ((1 / random2 - 1) * (max - min) / (1 / m - 1) + min + 0.5);
}
sum += integral2;
//最大最小值
if (integral2 > statisticalMax) {
statisticalMax = integral2;
}
if (integral2 < statisticalMin) {
statisticalMin = integral2;
}
//統計
int distributionsIndex = (integral2 - min) * 10 / (max - min);
statisticalDistributions[distributionsIndex] += 1;
}
System.out.println("随機數平均值：" + sum / totalCount);
System.out.println("随機數最大值：" + statisticalMax + "随機數最小值：" + statisticalMin);
System.out.println("每1/10的資料量分布：" + Arrays.toString(statisticalDistributions));//第11個直接是max的數量
}
現在就請盡情的揮灑吧。
其實真正的代碼連5行都沒有😂，但從無到有的邏輯真的夠喝幾天的了...
![Java小案例——随機數猜測随機數猜測[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)