什麼是激活函數
在神經網絡中,我們會對所有的輸入進行權重求和,之後我們會在對結果施加一個函數,這個函數就是我們所說的激活函數。如下圖所示。
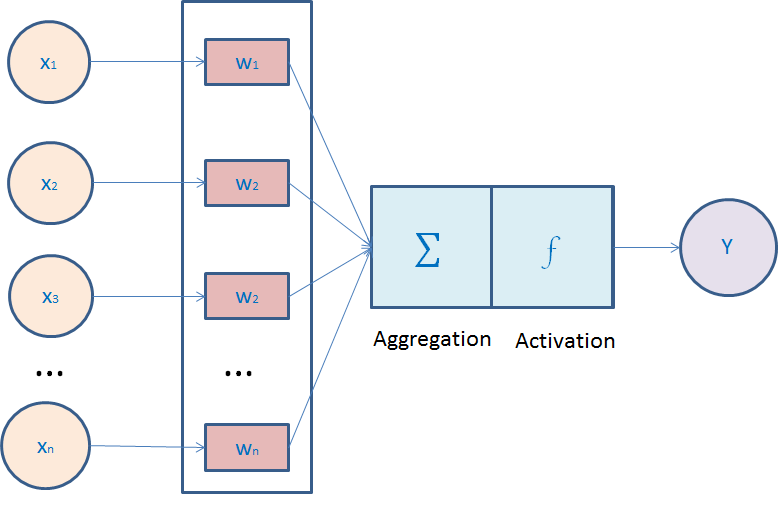
為什麼使用激活函數
我們使用激活函數并不是真的激活什麼,這隻是一個抽象概念,使用激活函數時為了讓中間輸出多樣化,能夠處理更複雜的問題。
如果不适用結果函數的話,每一層最後輸出的都是上一層輸入的線性函數,不管加多少層神經網絡,我們最後的輸出也隻是最開始輸入資料的線性組合而已。激活函數給神經元引入了非線性因素,當加入多層神經網絡時,就可以讓神經網絡拟合任何線性函數及非線性函數,進而使得神經網絡可以适用于更多的非線性問題,而不僅僅是線性問題。
有論文中把激活函數定義為一個幾乎處處可微的函數f: R->R
有哪些激活函數
對于神經網絡,一版我們會使用三種激活函數:Sigmoid函數、Tanh函數、ReLU函數。
基本概念:
飽和:
當函數f(x)滿足:
時,稱為右飽和;
當函數f(x)滿足:
時,稱為左飽和。
當f(x)同時滿足左飽和及右飽和時,稱為飽和。
軟包和與硬包和:
在飽和定義的基礎上,如果存在常數c1,當x>c1時候恒滿足
,稱之為右硬飽和;同樣的,如果存在c2,當x<c2時恒滿足
,稱之為左硬飽和。如果同時滿足了左飽和,又滿足了右飽和,稱之為硬包和。相對的,隻有在x趨于極值時才能滿足f(x)的倒數為0,則成為軟飽和。
1. Sigmoid 函數
sigmoid 曾經風靡一時,但是由于sigmoid有自身的缺陷,現在用的比較少了。
函數公式如下:
,相應的
函數曲線如下:
優點:
<1> Sigmoid的取值範圍在(0, 1),而且是單調遞增,比較容易優化
<2> Sigmoid求導比較容易,可以直接推導得出。
缺點:
<1> Sigmoid函數收斂比較緩慢
<2> 由于Sigmoid是軟飽和,容易産生梯度消失,對于深度網絡訓練不太适合(從圖上sigmoid的導數可以看出當x趨于無窮大的時候,也會使導數趨于0)
<3> Sigmoid函數并不是以(0,0)為中心點
2. Tanh函數
tanh為雙切正切曲線,過(0,0)點。相比Sigmoid函數,更傾向于用tanh函數
函數公式:
相應的
函數曲線如下:
優點:
<1> 函數輸出以(0,0)為中學
<2> 收斂速度相對于Sigmoid更快
缺點:
<1> tanh并沒有解決sigmoid梯度消失的問題
3. ReLU函數
最近這幾年很常用的激活函數。
公式如下:
圖形圖像:
優點:
<1> 在SGD中收斂速度要比Sigmoid和tanh快很多
<2> 有效的緩解了梯度消失問題
<3> 對神經網絡可以使用稀疏表達
<4> 對于無監督學習,也能獲得很好的效果
缺點:
<1> 在訓練過程中容易出現神經元失望,之後梯度永遠為0的情況。比如一個特别大的梯度結果神經元之後,我們調整權重參數,就會造成這個ReLU神經元對後來來的輸入永遠都不會被激活,這個神經元的梯度永遠都會是0,造成不可逆的死亡。
參考:http://www.cnblogs.com/rgvb178/p/6055213.html