1.系統基本原理分析
1.1系統設計要求
将WAV 格式的模拟音頻信号轉換為數字信号,WAV格式的檔案自己選擇。
下面是需要完成的具體部分:
Encoder: filter bank(32) Decoder: huffman decoding
DCT/quantization IDCT/inverse quantiser
Huffman coding inverse filter bank
課題的輸出要求及結果:
- 讀取 WAV 格式的檔案(沒有壓縮過的)
- 用Encoder 完成信号的壓縮
- 顯示并對比經過壓縮後的信号的存儲空間減小了
- 用Decoder 完成信号的解碼
- 在MATLAB 裡經解碼後的聲音播放出來
1.2 系統設計方案
Encoder: filter bank(32) Decoder: huffman decoding
DCT/quantization IDCT/inverse quantiser
Huffman coding inverse filter bank
具體的理論分析與代碼在2部分結合給出。
2.系統代碼設計
·語音讀取子產品
語音讀取的代碼如下所示:
function [x,Fs,nbits] = func_readwav(resources);
[x,Fs,nbits]=wavread(resources);
sound(x,Fs,nbits);
其波形如下所示:
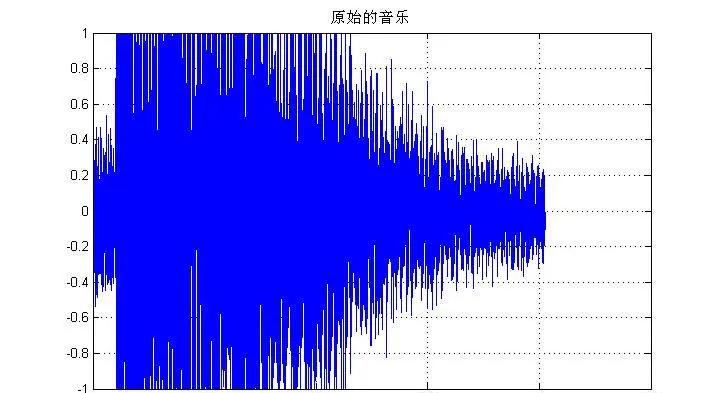
·濾波器與濾波器反變化
用窗函數法設計FIR濾波器組的基本思路為:
(1)根據所要求的分析頻率範圍和頻率分辨率選擇一組分析頻率ωk及相對應的原型理想低通濾波器的截止頻率ωck(k=0,1,…,L-1),L為濾波器組的通道數,得出理想帶通濾波器組的複合頻率響應。
(2)用窗函數法近似實作各個理想帶通濾波器。實際的複合頻率響應等于理想複合頻率響應與設計窗的頻率特性的卷積。在用窗函數法設計FIR濾波器時,還需要知道通帶内的紋波幅度δ,它可以根據阻帶衰減量As的要求來确定,通常的典型值為
As=-20lgδ=40∽60 (1)
如果選擇Kaiser窗,參數β的計算公式為
當As >50時,β=0.1102(As-8.7);
當21<As <50時,β=0.5845(As-21)0.5+0.07886(As-21)。 (2)
濾波器的階數為
M=(As-7.95)/14.36△F+1 3)
式中△F是歸一化過渡帶寬,即△F=△f•T,而
△f=△ω/2π (4)
過渡帶寬△ω的選擇根據對每個濾波器的頻率分辨率要求來決定,必須滿足限制條件
△ωk<2ωck (5)
如果各通道采用相同的設計窗,保證中心頻率及帶寬的選擇能覆寫-π到π頻率範圍(不管濾波器的中心頻率和帶寬如何分布),那麼最終得到的實際複合響應一定是理想的,即具有平坦幅度和線性相位。
首先計算各個通道下的濾波器H0,H1,H2,。。。。。H31。
然後分别進行濾波。得到各個通道下的濾波效果;
反濾波過程。
g0=-wrev(H(1,:));
g1=-wrev(H(2,:));
…………
首先對各個H,取逆。然後作為反濾波器函數G。
然後再次分别進行濾波進而得到各個通道下的濾波後的資料,然後将各個通道下的資料相加得到原始的信号。
load H.mat;
if select == 1
g0=-wrev(H(1,:));
g1=-wrev(H(2,:));
g2=-wrev(H(3,:));
g3=-wrev(H(4,:));
x_recon=filter(g0,1,datas(1,:))+filter(g1,1,datas(2,:))+filter(g2,1,datas(3,:))+filter(g3,1,datas(4,:));
end
if select == 0
x_recon = datas;
end
注意,由于本系統采用32子通道的話将耗費大量的仿真時間,是以,本系統暫時采用的4通道的仿真模式。其濾波器組的仿真結果如下所示;
【采用32個通道的時候,仿真時間超級長,是以先給你做出基本的東西,如果沒什麼問題,改為32個通道就OK。】
·DCT與IDCT
我們在這裡使用MATLAB内部的dct函數。這裡就不多做介紹了。
這裡比較簡單,就是MATLAB自帶的函數,dct和idct兩個函數。