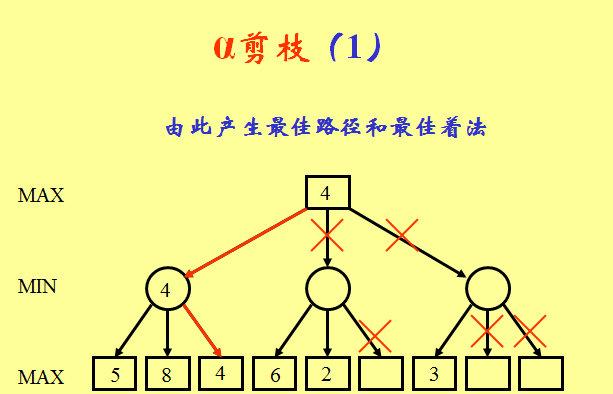
•一種基于剪枝( α-βcut-off)的深度優先搜尋(depth-first search)。 •将走棋方定為MAX方,因為它選擇着法時總是對其子節點的評估值取極大值,即選擇對自己最為有利的着法; •将應對方定為MIN方,因為它走棋時需要對其子節點的評估值取極小值,即選擇對走棋方最為不利的、最有鉗制作用的着法。 •在對博弈樹采取深度優先的搜尋政策時,從左路分枝的葉節點倒推得到某一層MAX節點的值,可表示到此為止得以“落實”的着法最佳值,記為α。 •顯然此值可作為MAX方着法名額的下界。 •在搜尋此MAX節點的其它子節點,即探讨另一着法時,如果發現一個回合(2步棋)之後評估值變差,即孫節點評估值低于下界α值,則便可以剪掉此枝(以該子節點為根的子樹),即不再考慮此“軟着”的延伸。 •此類剪枝稱為α剪枝。
•同理,由左路分枝的葉節點倒推得到某一層MIN節點的值,可表示到此為止對方着法的鉗制值,記為β。 •顯然此β值可作為MAX方無法實作着法名額的上界。 •在搜尋該MIN節點的其它子節點,即探讨另外着法時,如果發現一個回合之後鉗制局面減弱,即孫節點評估值高于上界β值,則便可以剪掉此枝,即不再考慮此“軟着”的延伸。 •此類剪枝稱為β剪枝。
、
•α-β剪枝是根據極大-極小搜尋規則的進行的,雖然它沒有周遊某些子樹的大量節點,但它仍不失為窮盡搜尋的本性。 •α-β剪枝原理中得知: α值可作為MAX方可實作着法名額的下界 β值可作為MAX方無法實作着法名額的上界 于是由α和β可以形成一個MAX方候選着法的視窗 也便出現了各種各樣的α-β視窗搜尋算法。
轉載于:https://www.cnblogs.com/IThaitian/p/3616550.html