歐式距離和餘弦距離

1、歐氏距離（歐幾裡得距離，Euclidean Distance）：是最常見的距離度量，衡量的是多元空間中各個點之間的絕對距離。公式如下：

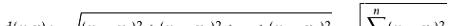
2、闵氏距離：又叫做闵可夫斯基距離,是歐氏空間中的一種測度，被看做是歐氏距離的一種推廣，歐氏距離是闵可夫斯基距離的一種特殊情況。公式如下：

公式中，當p = 2時，即歐氏距離；當p = 1時，即曼哈頓距離；當

，即切比雪夫距離；

A至B的距離中，綠色的線為歐氏距離，紅色和黃色的線為曼哈頓距離；

python實作：

import numpy as np

#生成10行浮點數，從0-1中随機
x = np.random.random(10)
y = np.random.random(10)

#方法一：numpy中提供了範數的計算工具：linalg.norm()
dist1 = np.linalg.norm(x - y)

#方法二
dist2 = np.sqrt(np.sum(np.square(x - y)))



print('x':x)

print('y':y)

print('dist1':dist1)

print('dist2':dist2)





# 計算歐式距離
def euclideanDistance(instance1, instance2, length):
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]), 2)
    return math.sqrt(distance)

           

3、餘弦距離

餘弦相似度用向量空間中兩個向量夾角的餘弦值作為衡量兩個個體間差異的大小。相比距離度量，餘弦相似度更加注重兩個向量在方向上的差異，而非距離或長度上。公式如下：

 假設||A||、||B||表示向量A、B的2範數，例如向量[1,2,3]的2範數為：

 python實作：

import numpy as np
from scipy.spatial.distance import pdist 
x=np.random.random(10)
y=np.random.random(10) 
# 方法一，np.dot,做矩陣乘法
dist1 = 1 - np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y)) 
# 方法二
dist2 = pdist(np.vstack([x,y]),'cosine') 
print('x':x)
print('y':y)
print('dist1':dist1)
print('dist2':dist2)
           

參考來源：

https://blog.csdn.net/Mr_EvanChen/article/details/77511312

https://cloud.tencent.com/developer/article/1487432