機器學習實戰之--regression

前面主要講到了分類問題，從這節開始，進入到回歸的學習。這節主要介紹幾個常用的數值回歸算法。

1、線性回歸

資料的線性拟合

平方誤差損失函數：

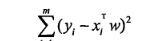
回歸系數：

主要算法實作：

def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == :
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws
           

2、局部權重線性回歸

由于線性回歸可能的欠拟合，引入局部權重線性回歸，根據距離訓練樣本和預測樣本之間的距離不同，而給定不同的權值。

為了表示上面的權值，引入核，常用的核為高斯核：

k取不同值時，與權重w的關系

回歸系數：

主要算法實作：

def lwlr(testPoint,xArr,yArr,k=):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[]
    weights = mat(eye((m)))
    for j in range(m):                      #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]     #
        weights[j,j] = exp(diffMat*diffMat.T/(-*k**))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == :
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr,xArr,yArr,k=):  #loops over all the data points and applies lwlr to each one
    m = shape(testArr)[]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

def lwlrTestPlot(xArr,yArr,k=):  #same thing as lwlrTest except it sorts X first
    yHat = zeros(shape(yArr))       #easier for plotting
    xCopy = mat(xArr)
    xCopy.sort()
    for i in range(shape(xArr)[]):
        yHat[i] = lwlr(xCopy[i],xArr,yArr,k)
    return yHat,xCopy
           

3、嶺回歸和逐漸線性回歸

如果特征數>樣本個數（m>n）怎麼辦？（此時非滿秩矩陣，矩陣不能求逆），一開始為了解決這個問題而引入了縮減系數的方法，嶺回歸就是其中的一種。簡單來說嶺回歸就是在矩陣X’*T後加入一個lamda*I，使之成為一個滿秩矩陣。嶺回歸也用于在估計中加入偏差，以便能得到更好的估計。這裡通過引入lamda來限制所有的w之和，通過引入該懲罰項，能夠減少不重要的參數，這一技術在統計學上稱為縮減技術。

回歸系數：![這裡寫圖檔描述](https://img-blog.csdn.net

主要代碼實作：（資料要做标準化處理，思考一下上面時候要用到資料标準化？損失函數，權重和）

def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays
    return ((yArr-yHatArr)**).sum()

def ridgeRegres(xMat,yMat,lam=):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[])*lam
    if linalg.det(denom) == :
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T*yMat)
    return ws

def ridgeTest(xArr,yArr):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,)
    yMat = yMat - yMean     #to eliminate X0 take mean off of Y
    #regularize X's
    xMeans = mean(xMat,)   #calc mean then subtract it off
    xVar = var(xMat,)      #calc variance of Xi then divide by it
    xMat = (xMat - xMeans)/xVar
    numTestPts = 
    wMat = zeros((numTestPts,shape(xMat)[]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-))
        wMat[i,:]=ws.T
    return wMat

def regularize(xMat):#regularize by columns
    inMat = xMat.copy()
    inMeans = mean(inMat,)   #calc mean then subtract it off
    inVar = var(inMat,)      #calc variance of Xi then divide by it
    inMat = (inMat - inMeans)/inVar
    return inMat
           

向前逐漸回歸：

算法僞代碼

def stageWise(xArr,yArr,eps=,numIt=):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,)
    yMat = yMat - yMean     #can also regularize ys but will get smaller coef
    xMat = regularize(xMat)
    m,n=shape(xMat)
    #returnMat = zeros((numIt,n)) #testing code remove
    ws = zeros((n,)); wsTest = ws.copy(); wsMax = ws.copy()
    for i in range(numIt):
        print ws.T
        lowestError = inf; 
        for j in range(n):
            for sign in [-,]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign
                yTest = xMat*wsTest
                rssE = rssError(yMat.A,yTest.A)
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        #returnMat[i,:]=ws.T
    #return returnMat
           

4、權衡方差和偏差

能挖掘出哪些特征是重要的，哪些特征是不重要的

算法實作：

def crossValidation(xArr,yArr,numVal=):
    m = len(yArr)                           
    indexList = range(m)
    errorMat = zeros((numVal,))#create error mat 30columns numVal rows
    for i in range(numVal):
        trainX=[]; trainY=[]
        testX = []; testY = []
        random.shuffle(indexList)
        for j in range(m):#create training set based on first 90% of values in indexList
            if j < m*: 
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        wMat = ridgeTest(trainX,trainY)    #get 30 weight vectors from ridge
        for k in range():#loop over all of the ridge estimates
            matTestX = mat(testX); matTrainX=mat(trainX)
            meanTrain = mean(matTrainX,)
            varTrain = var(matTrainX,)
            matTestX = (matTestX-meanTrain)/varTrain #regularize test with training params
            yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)#test ridge results and store
            errorMat[i,k]=rssError(yEst.T.A,array(testY))
            #print errorMat[i,k]
    meanErrors = mean(errorMat,)#calc avg performance of the different ridge weight vectors
    minMean = float(min(meanErrors))
    bestWeights = wMat[nonzero(meanErrors==minMean)]
    #can unregularize to get model
    #when we regularized we wrote Xreg = (x-meanX)/var(x)
    #we can now write in terms of x not Xreg:  x*w/var(x) - meanX/var(x) +meanY
    xMat = mat(xArr); yMat=mat(yArr).T
    meanX = mean(xMat,); varX = var(xMat,)
    unReg = bestWeights/varX
    print "the best model from Ridge Regression is:\n",unReg
    print "with constant term: ",-*sum(multiply(meanX,unReg)) + mean(yMat)