常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 第38講 泰勒級數
Taylor's series
34 泰勒級數v.youku.com
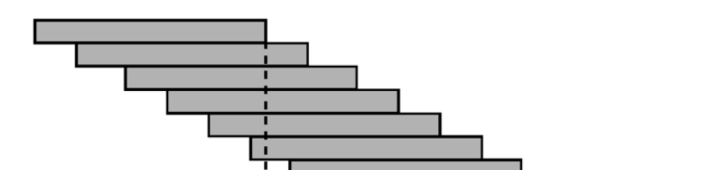
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 例 ：積木問題。
将積木堆積起來，上層積木依次側移向外，能否将最上層積木完全移動至最底層積木的左側，即頂層積木的右側邊線超出底層積木的左側邊線。或者問不斷累積這種側移，是會達到某個極限還是沒有極限。
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 技巧在于從最上層開始進行計算以達到最佳政策。這種方法在計算中稱為“貪婪算法”，在每一步都達到最大的可能，但是隻能從最上層開始使用這種政策。為了讨論友善，将積木長度定為2，那麼1号積木最大探出量就在它的重心位置
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ；疊加2号積木後的最大位移量就在1号和2号的共同重心位置。
按照此方法進行，當累加到第N塊時，位移量為
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，再累加至第 N+1塊時則有
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。
将前 N塊和最後一塊分别計算重力力矩加和除以所有積木的重量 N+1，就得到了所有積木的總體重心。
1号積木最大探出量為
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ；疊加2号積木後的最大位移量為
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ；疊加第三塊積木後，則有
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。是以得到
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。是以位移位置就是調和級數的累積和
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。則根據上次課的推導有
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。是以最大位移是發散的。并且這個數量關系給出了所達到距離和所需積木數 N之間的關系。例如想要橫跨整張桌子，則要達到距離為24，是以有
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，計算可得到
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。這些積木摞起來的高度為
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，這是地球到月亮距離的兩倍。疊起來的積木的邊緣所構成的曲線形狀就是對數曲線，從這個計算也可以看出對數曲線的增長是非常緩慢的。
已經學過一個幂級數
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。它也就是幾何級數。
令
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，則用 x乘以等式兩側得
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。與前式相減得到
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，整理可得
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。注意：證明過程要求級數是收斂的。
幂級數
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。 x的取值若在收斂半徑之内
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，即在收斂點集區間
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 之内時，級數收斂。
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 為級數的發散區域。
對于幂級數而言，當x在收斂半徑之内時，有
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，它以指數速度衰減；在收斂半徑之外，則
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 不趨向于零。
對于收斂的幂級數可以進行運算，其運算法則與多項式相同。可以進行加法、乘法、除法、函數複合還有微分和積分。
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 泰勒公式是用特殊系數的幂級數形式來表示函數的一種方法。例如函數
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，本身并不是一個類似于多項式的狀态，通過給定特定的系數可以将之表示為級數的狀态。泰勒公式
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 由
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 得到
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。可知參數通式為
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。
例 ：
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 例 ：在近似公式中得到了
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 ，
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 。通過泰勒級數可以得到完全的函數公式。
常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 常用的收斂級數整理_MIT—單變量微積分筆記38 泰勒級數 通過比較泰勒公式形式可以知道，正弦函數、餘弦函數和e的指數函數是同一種類型的函數。
