常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 第38讲 泰勒级数
Taylor's series
34 泰勒级数v.youku.com
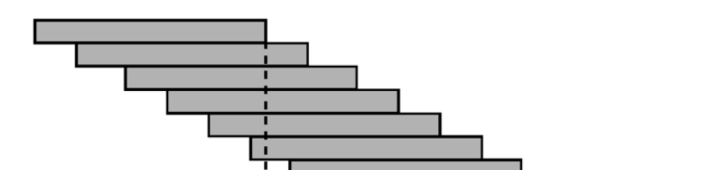
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 例 ：积木问题。
将积木堆积起来，上层积木依次侧移向外，能否将最上层积木完全移动至最底层积木的左侧，即顶层积木的右侧边线超出底层积木的左侧边线。或者问不断累积这种侧移，是会达到某个极限还是没有极限。
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 技巧在于从最上层开始进行计算以达到最佳策略。这种方法在计算中称为“贪婪算法”，在每一步都达到最大的可能，但是只能从最上层开始使用这种策略。为了讨论方便，将积木长度定为2，那么1号积木最大探出量就在它的重心位置
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ；叠加2号积木后的最大位移量就在1号和2号的共同重心位置。
按照此方法进行，当累加到第N块时，位移量为
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，再累加至第 N+1块时则有
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。
将前 N块和最后一块分别计算重力力矩加和除以所有积木的重量 N+1，就得到了所有积木的总体重心。
1号积木最大探出量为
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ；叠加2号积木后的最大位移量为
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ；叠加第三块积木后，则有
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。因此得到
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。因此位移位置就是调和级数的累积和
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。则根据上次课的推导有
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。因此最大位移是发散的。并且这个数量关系给出了所达到距离和所需积木数 N之间的关系。例如想要横跨整张桌子，则要达到距离为24，因此有
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，计算可得到
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。这些积木摞起来的高度为
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，这是地球到月亮距离的两倍。叠起来的积木的边缘所构成的曲线形状就是对数曲线，从这个计算也可以看出对数曲线的增长是非常缓慢的。
已经学过一个幂级数
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。它也就是几何级数。
令
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，则用 x乘以等式两侧得
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。与前式相减得到
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，整理可得
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。注意：证明过程要求级数是收敛的。
幂级数
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。 x的取值若在收敛半径之内
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，即在收敛点集区间
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 之内时，级数收敛。
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 为级数的发散区域。
对于幂级数而言，当x在收敛半径之内时，有
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，它以指数速度衰减；在收敛半径之外，则
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 不趋向于零。
对于收敛的幂级数可以进行运算，其运算法则与多项式相同。可以进行加法、乘法、除法、函数复合还有微分和积分。
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 泰勒公式是用特殊系数的幂级数形式来表示函数的一种方法。例如函数
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，本身并不是一个类似于多项式的状态，通过给定特定的系数可以将之表示为级数的状态。泰勒公式
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 由
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 得到
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。可知参数通式为
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。
例 ：
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 例 ：在近似公式中得到了
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 ，
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 。通过泰勒级数可以得到完全的函数公式。
常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 常用的收敛级数整理_MIT—单变量微积分笔记38 泰勒级数 通过比较泰勒公式形式可以知道，正弦函数、余弦函数和e的指数函数是同一种类型的函数。
