文章目錄
- 狄拉克函數
- 光滑近似
- Relu激活
- 取整函數
- 文章小結
- 轉載
在機器學習中,我們經常會碰到不光滑的函數,但我們的優化方法通常是基于梯度的,這意味着光滑的模型可能更利于優化(梯度是連續的),是以就有了尋找非光滑函數的光滑近似的需求。事實上,本部落格已經多次讨論過相關主題,比如
《尋求一個光滑的最大值函數》、
《函數光滑化雜談:不可導函數的可導逼近》等,但以往的讨論在方法上并沒有什麼通用性。
不過,筆者從最近的一篇論文《SAU: Smooth activation function using convolution with approximate identities》學習到了一種比較通用的思路:用狄拉克函數來構造光滑近似。通用到什麼程度呢?理論上有可數個間斷點的函數都可以用它來構造光滑近似!個人感覺還是非常有意思的。
注:部分積分的計算可以參考常見積分求解
狄拉克函數
在很早之前的文章《詭異的Dirac函數》中,我們就介紹過狄拉克函數了。在現代數學中,狄拉克函數被定義為一個“泛函”而不是“函數”,但對于大多數讀者來說,将它當作函數來了解是比較容易接受的。
簡單來說,狄拉克函數
滿足:
1、
2、
3、
直覺來看,
可以看成一個連續型的機率密度函數,采樣空間為全體實數
,但是隻有
處機率非零,也即均值為
、方差也為
,是以從中采樣必然隻能采樣到
,是以成立如下恒等式:
或者
這可謂是狄拉克函數最重要的性質,也是我們後面主要用到的恒等式。
光滑近似
如果我們能找到
的一個光滑近似
,那麼根據(2),我們就有
由于
是光滑的,是以
也是光滑的,這也就是說,
就是
的一個光滑近似!這便是借助狄拉克函數的光滑近似來建構
的光滑近似的核心思路了,在這個過程中,對
的形式和連續性都沒有太多限制,比如允許
有可數個間斷點(如取整函數
)。
那麼狄拉克函數的光滑近似有哪些呢?現成的也有不少,比如:
或
簡單來說,就是找一個像正态分布那樣鐘形曲線的非負函數,想辦法讓鐘形的寬度逐漸趨于0,但保持積分為1。還有另一個思路是留意到
也就是說,狄拉克函數的積分是“機關階躍函數”
,如果我們能找到
的光滑近似,那麼将它求導就得到狄拉克函數的光滑近似。而
的光滑近似,就是所謂的“S形”曲線了,比如sigmoid函數
,是以我們有
常用的就是式(4)和式(7)兩個近似。
Relu激活
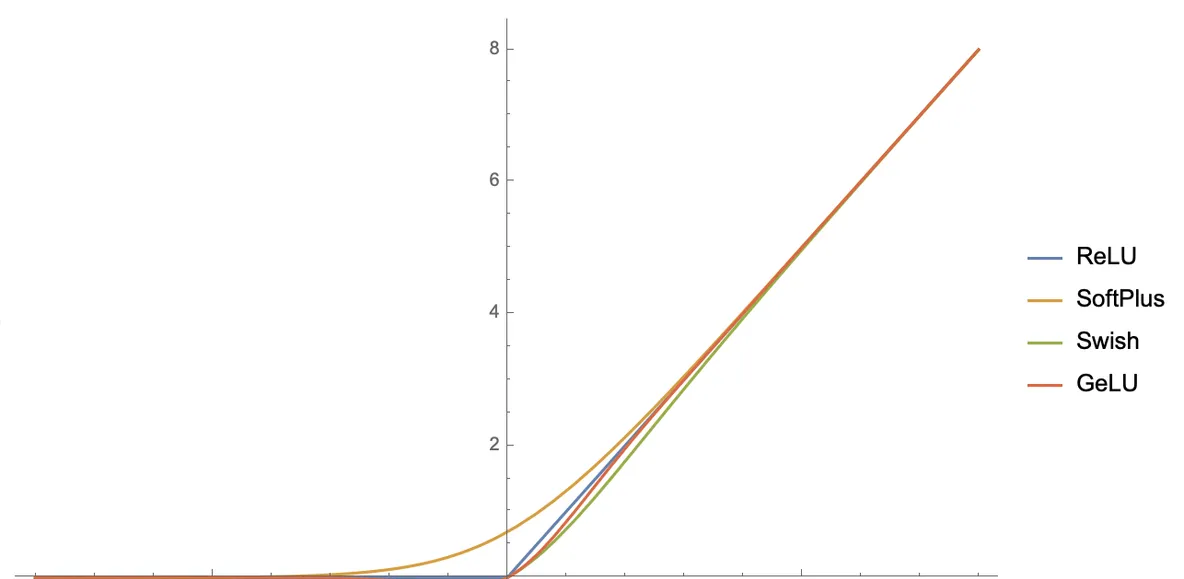
現在,我們就以上述思路為工具,推導ReLU激活函數
的各種光滑近似。
比如利用式(7),得到
當t=1時,這便是SoftPlus激活函數。
如果換用式(4),那麼結果是
這個ReLU的光滑近似貌似還沒被研究過。
當然,如果僅僅是ReLU函數的光滑近似,那麼還有更簡單的思路,比如留意到
,這裡的θ(x)就是前面提到的機關階躍函數,是以問題可以轉變為求θ(x)的光滑近似,我們已經知道sigmoid便是其中之一,是以很快得到
當
時,這便是Swish激活函數。而如果用(4)進行計算
的光滑近似,那麼就得到
當
時,就是GeLU激活函數。
取整函數
可能讀者覺得還不夠意思,畢竟上面推導出來的都是現成的東西,而且不借助狄拉克函數也能推導出來。現在我們就來補充一個不怎麼平凡的例子:取整函數的光滑近似。
取整函數分上取整和下取整兩種,它們定義上有所不同,但是沒有本質差別,這裡以下取整為例子,我們記為
假設
為狄拉克函數的某個光滑近似,那麼
設
的原函數為
,那麼
關于
的原函數就是
,于是有
對于
我們有
和
,是以假設我們關心的範圍滿足
,那麼
和
,是以此時:
用
作為例子,取
,結果如下:
可以看到,确實與
蠻近似的,增大
能進一步提高近似程度。