無人駕駛的規劃與控制（四）——回報控制

文章目錄

• 1 自行車模型
• 2 PID回報控制
• • 2.1 橫向控制
  • 2.2 縱向控制

1 自行車模型

在自行車模型中，我們假設車輛姿态處于一個二維的平面坐标系内，車輛的姿态可以由位移（position）和車身夾角（heading）完全描述，并且前後輪由一個剛性（rigid）軸連接配接，前輪可轉動，後輪隻能直行。

自行車模型的一個重要特征是：如果車輛不向前移動，就不能橫向位移，稱為非完整性限制（nonholonomic constraint）。

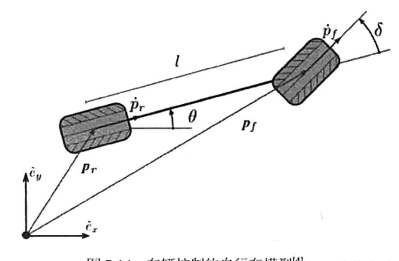
符号	含義
e ‾ x , e ‾ y \overline{e}_{x},\overline{e}_{y} ex​,ey​	x和y方向的機關向量
p r p_{r} pr​	position rear tyre 後輪所在位置的向量
p ˙ r \dot{p}_{r} p˙​r​	後輪地面接觸點瞬時速度向量
p f p_{f} pf​	position front tyre 前輪所在位置的向量
p ˙ f \dot{p}_{f} p˙​f​	前輪地面接觸點瞬時速度向量
θ \theta θ	車身的朝向角，即後輪朝向角 P ˙ r \dot{P}_r P˙r​和 e ‾ x \overline{e}_x ex​的夾角
δ \delta δ	方向盤轉角，前輪朝向和車身朝向的夾角
l l l	剛性軸長度

這樣後輪的x方向速度分量 x ˙ r \dot{x}_r x˙r​，y方向速度分量 y ˙ r \dot{y}_r y˙​r​，和朝向角可以表示為：

x ˙ r = v r cos ⁡ ( θ ) \dot{x}_{r}=v_{r} \cos (\theta) x˙r​=vr​cos(θ)

y ˙ r = v r sin ⁡ ( θ ) \dot{y}_{r}=v_{r} \sin (\theta) y˙​r​=vr​sin(θ)

θ = v r tan ⁡ ( δ ) / l \theta=v_{r} \tan (\delta) / l θ=vr​tan(δ)/l

同理，前輪的x方向速度分量 x ˙ f \dot{x}_f x˙f​，y方向速度分量 y ˙ f \dot{y}_f y˙​f​，和朝向角可以表示為：

x ˙ f = v f cos ⁡ ( θ + δ ) \dot{x}_{f}=v_{f} \cos (\theta+\delta) x˙f​=vf​cos(θ+δ)

y ˙ f = v f sin ⁡ ( θ + δ ) \dot{y}_{f}=v_{f} \sin (\theta+\delta) y˙​f​=vf​sin(θ+δ)

θ = v f sin ⁡ ( δ ) / l \theta=v_{f} \sin (\delta) / l θ=vf​sin(δ)/l

前後輪的切向速度滿足： v r = v f cos ⁡ ( δ ) v_{r}=v_{f} \cos (\delta) vr​=vf​cos(δ)

在這樣的車輛模型下，回報控制需要解決的問題之一，就是尋找滿足車輛動态姿态限制的方向盤轉角 δ ∈ [ δ m i n , δ m a x ] \delta\in[\delta_{min},\delta_{max}] δ∈[δmin​,δmax​]和前向速度 v r ∈ [ v m i n , v m a x ] v_r\in[v_{min},v_{max}] vr​∈[vmin​,vmax​]。

2 PID回報控制

無人車回報控制子產品的任務，是控制車輛盡可能遵循上遊動作規劃（軌迹和速度）出的時空軌迹。

這裡使用兩個PID控制器分别控制方向盤轉角 δ \delta δ以及前進速度 v s v_s vs​。

2.1 橫向控制

橫向控制主要跟蹤的變量誤差主要是軌迹的橫向誤差，和角度誤差。

在n采樣時刻，控制方向盤轉角的PID控制器如下：

δ n = K 1 θ e + K 2 l e / V s + K 3 i e + K 4 ∑ i = 1 n l e Δ t \delta_{n}=K_{1} \theta_{e}+K_{2} l_{e} / V_{s}+K_{3} i_{e}+K_{4} \sum_{i=1}^{n} l_{e} \Delta t δn​=K1​θe​+K2​le​/Vs​+K3​ie​+K4​i=1∑n​le​Δt

符号	說明
θ e \theta_e θe​	目前車朝向，和基準軌迹點（Reference Point）之間的跟蹤角度誤差
l e l_e le​	橫向位置和基準點軌迹之間的距離誤差
V s V_s Vs​	車輛在縱向方向的速度

2.2 縱向控制

縱向控制主要跟蹤的速度誤差，其中速度誤差是軌迹曲率和基準軌迹點曲率的函數：

V e = − f ( k  Vehicle  , k  Reference  ) V_e=-f\left(k_{\text { Vehicle }}, k_{\text { Reference }}\right) Ve​=−f(k Vehicle ​,k Reference ​)

是以前進速度的PID控制器可以寫成：

U V = K P V e + K I ∑ V e Δ t + K D Δ V e / Δ t U_{V}=K_{P} V_{e}+K_{I} \sum V_{e} \Delta t+K_{D} \Delta V_{e} / \Delta t UV​=KP​Ve​+KI​∑Ve​Δt+KD​ΔVe​/Δt

符号	說明
k  Vehicle  k_{\text { Vehicle }} k Vehicle ​	車輛目前的軌迹點曲率
k  Reference  k_{\text { Reference }} k Reference ​	基準軌迹點的基準點曲率

參考文章

《第一本無人駕駛技術書》劉少山

在Typora中輸入公式

Typora開啟行内公式

常用數學符号的 LaTeX 表示方法

一份不太簡短的LATEX2ε介紹【精華】