Paper-4 精讀 GCL（2016 ICML）

Guided Cost Learning

• 概述與定位
• 一、GCL的基礎知識
• • 1.1 軌迹的模組化方式---PGM
  • 1.2 軌迹的模組化方式---Policy
• 二、文章的主要邏輯
• 三、實驗小細節
• 四、總結

概述與定位

1. 這是一個Inverse RL的問題，也稱為Inverse Optimal Control，學習的目标是從expert demonstrations中得到一個cost function即reward function
2. 傳統IRL面臨兩個問題，一個是需要設計cost function的形式，另一個是在unknown dynamics即model-free的情況下，學習cost function面臨一定的困難
3. 是以這篇文paper，利用NN作為cost function避免設計的麻煩，再用sample-based approximation的方式去學這個cost function

基礎理論

深度強化學習CS285 lec13-lec15 （下）

一、GCL的基礎知識

設定：我們從reward的角度開始介紹這個問題，reward與cost的角度實際上是相同的，之是以有變化是因為有時候在控制論的語境用cost，有時候在standard RL的語境用reward。現在開始接近最近的文章就統一reward吧

1.1 軌迹的模組化方式—PGM

之前在Control As Inference中提過，有一堆專家資料即expert trajectories，也可以了解成是optimal behaviors，引入了一個optimality variable來專門對專家行為進行模組化： p ( O t ∣ s t , a t ) = e x p ( r ( s t , a t ) ) = e x p ( − c ( s t , a t ) ) p(O_t|s_t,a_t)=exp(r(s_t,a_t))=exp(-c(s_t,a_t)) p(Ot​∣st​,at​)=exp(r(st​,at​))=exp(−c(st​,at​))

p ( τ ∣ O 1 : T ) = p ( τ , O 1 : T ) p ( O 1 : T ) ∝ p ( τ , O 1 : T ) = p ( τ ) p ( O 1 : T ∣ τ ) = p ( τ ) e x p ( ∑ t = 1 T r ( s t , a t ) ) = [ p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] e x p ( ∑ t = 1 T r ( s t , a t ) ) \begin{aligned} p(\tau|O_{1:T})=\frac{p(\tau,O_{1:T})}{p(O_{1:T})}&\propto p(\tau,O_{1:T})\\ &=p(\tau)p(O_{1:T}|\tau)\\ &=p(\tau)exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big)\\ &=\Big[p(s_1)\prod_{t=1}^{T}p(s_{t+1}|s_t,a_t)\Big]exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) \end{aligned} p(τ∣O1:T​)=p(O1:T​)p(τ,O1:T​)​​∝p(τ,O1:T​)=p(τ)p(O1:T​∣τ)=p(τ)exp(t=1∑T​r(st​,at​))=[p(s1​)t=1∏T​p(st+1​∣st​,at​)]exp(t=1∑T​r(st​,at​))​

這個感覺很奇怪，怎麼 p ( τ ) p(\tau) p(τ)中的policy沒了？因為這個是基于PGM的模組化，專家資料中直接就有了state與action，不需要去管state與action之間的映射。如圖：

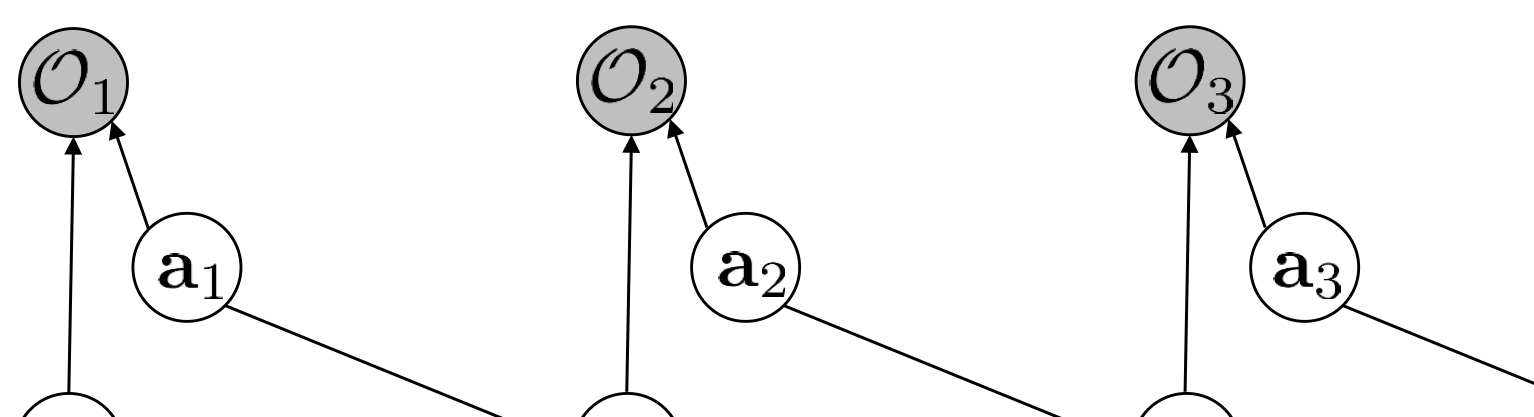
那現在我們想要參數化的是reward function，是以有：

p ( τ ∣ O 1 : T , ψ ) ∝ p ( τ ) e x p ( ∑ t = 1 T r ψ ( s t , a t ) ) = p ( τ ) e x p ( r ψ ( τ ) ) \begin{aligned} p(\tau|O_{1:T},\psi)&\propto p(\tau)exp\Big(\sum_{t=1}^Tr_\psi(s_t,a_t)\Big)\\ &=p(\tau)exp(r_\psi(\tau)) \end{aligned} p(τ∣O1:T​,ψ)​∝p(τ)exp(t=1∑T​rψ​(st​,at​))=p(τ)exp(rψ​(τ))​

現在有專家資料 τ ( i ) \tau^{(i)} τ(i)，Maximum Likelihood Learning去學習reward：

max ⁡ ψ L ( ψ ) = max ⁡ ψ 1 N ∑ i = 1 N l o g p ( τ ( i ) ∣ O 1 : T , ψ ) = max ⁡ ψ 1 N ∑ i = 1 N r ψ ( τ ( i ) ) − l o g Z \max_\psi L(\psi)=\max_\psi \frac{1}{N}\sum_{i=1}^Nlogp(\tau^{(i)}|O_{1:T},\psi)=\max_\psi \frac{1}{N}\sum_{i=1}^Nr_\psi(\tau^{(i)})-logZ ψmax​L(ψ)=ψmax​N1​i=1∑N​logp(τ(i)∣O1:T​,ψ)=ψmax​N1​i=1∑N​rψ​(τ(i))−logZ其中 Z Z Z為軌迹的歸一化因子，即Partition function，因為要去掉正比 ∝ \propto ∝的符号.

Z = ∫ p ( τ ) e x p ( r ψ ( τ ) ) d τ Z=\int p(\tau)exp\big(r_\psi(\tau)\big)d\tau Z=∫p(τ)exp(rψ​(τ))dτ

1.2 軌迹的模組化方式—Policy

下面這個是Standard RL的正常模組化方式：

p ( τ ) = p ( s 1 ) ∏ t = 1 T π ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) p(\tau)=p(s_1)\prod_{t=1}^T\pi(a_t|s_t)p(s_{t+1}|s_t,a_t) p(τ)=p(s1​)t=1∏T​π(at​∣st​)p(st+1​∣st​,at​)

實際上還有一個reward的，不過它是一個scalar，不是一個要學習的函數，是以就忽略了。這裡的trajectory是由policy與dynamics生成的，trajectory distribution是policy的一種表達。而上面PGM的模組化是對專家資料的“軌迹”分布進行了表達。

衆所周知，PGM最大的問題是partition function的積分求和難以計算的問題，是以就需要逼近。那怎麼逼近呢？是的，采用軌迹另一種建構方式Policy去逼近PGM的trajectory distribution，進而使partition function即 Z = ∫ p ( τ ) e x p ( r ψ ( τ ) ) d τ Z=\int p(\tau)exp\big(r_\psi(\tau)\big)d\tau Z=∫p(τ)exp(rψ​(τ))dτ變得可估計！

二、文章的主要邏輯

Partition Function的估計，論文提到有Laplace Approximation、Value Function Approximation以及Samples的方式。Paper采用的就是基于Samples的方式對配分函數Z進行了估計，主要思路如下：

1. 先對問題的梯度進行公式展開

   ∇ ψ L ( ψ ) = ∇ ψ [ E τ ∼ π ∗ ( τ ) [ r ψ ( τ ) ] − l o g ∫ p ( τ ) e x p ( r ψ ( τ ) ) d τ ] = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − 1 Z ∫ p ( τ ) e x p ( r ψ ( τ ) ) ⏟ p ( τ ∣ O 1 : T , ψ ) ∇ ψ r ψ ( τ ) d τ = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] \begin{aligned} \nabla_\psi L(\psi)&=\nabla_\psi\Big[E_{\tau\sim\pi^*(\tau)}\big[r_\psi(\tau)\big]-log\int p(\tau)exp\big(r_\psi(\tau)\big)d\tau\Big]\\ &=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-\underbrace{\frac{1}{Z}\int p(\tau)exp\big(r_\psi(\tau)\big)}_{p(\tau|O_{1:T},\psi)}\nabla_\psi r_\psi(\tau)d\tau\\ &=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ \end{aligned} ∇ψ​L(ψ)​=∇ψ​[Eτ∼π∗(τ)​[rψ​(τ)]−log∫p(τ)exp(rψ​(τ))dτ]=Eτ∼π∗(τ)​[∇ψ​rψ​(τ)]−p(τ∣O1:T​,ψ)

   Z1​∫p(τ)exp(rψ​(τ))​​∇ψ​rψ​(τ)dτ=Eτ∼π∗(τ)​[∇ψ​rψ​(τ)]−Eτ∼p(τ∣O1:T​,ψ)​[∇ψ​rψ​(τ)]​

2. 以Policy的建構方式來表達第二項的 E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] E_{\tau\sim p(\tau|O_{1:T},\psi)}[\nabla_\psi r_\psi(\tau)] Eτ∼p(τ∣O1:T​,ψ)​[∇ψ​rψ​(τ)]

   E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] = E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ ∑ t = 1 T r ψ ( s t , a t ) ] = ∑ t = 1 T E ( s t , a t ) ∼ p ( s t , a t ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( s t , a t ) ] = ∑ t = 1 T E s t ∼ p ( s t ∣ O 1 : T , ψ ) , a t ∼ p ( a t ∣ s t , O 1 : T , ψ ) [ ∇ ψ r ψ ( s t , a t ) ] \begin{aligned} &E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ &=E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi \sum_{t=1}^T r_\psi(s_t,a_t) \big]\\ &=\sum_{t=1}^TE_{(s_t,a_t)\sim p(s_t,a_t|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(s_t,a_t)\big]\\ &=\sum_{t=1}^TE_{s_t\sim p(s_t|O_{1:T},\psi),a_t\sim p(a_t|s_t,O_{1:T},\psi)}\big[\nabla_\psi r_\psi(s_t,a_t)\big]\\ \end{aligned} ​Eτ∼p(τ∣O1:T​,ψ)​[∇ψ​rψ​(τ)]=Eτ∼p(τ∣O1:T​,ψ)​[∇ψ​t=1∑T​rψ​(st​,at​)]=t=1∑T​E(st​,at​)∼p(st​,at​∣O1:T​,ψ)​[∇ψ​rψ​(st​,at​)]=t=1∑T​Est​∼p(st​∣O1:T​,ψ),at​∼p(at​∣st​,O1:T​,ψ)​[∇ψ​rψ​(st​,at​)]​

3. Soft Optimal Policy即 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at​∣st​,O1:T​,ψ)樣本的獲得用另一個policy即 π θ ( a t ∣ s t ) \pi_\theta(a_t|s_t) πθ​(at​∣st​)去近似它，是以采用Importance Sampling的方式使用 π ( a t ∣ s t ) \pi(a_t|s_t) π(at​∣st​)中的軌迹樣本:

   ∇ ψ L ( ψ ) = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] ≈ 1 N ∑ i = 1 N ∇ ψ r ψ ( τ ( i ) ) − 1 ∑ j w j ∑ j = 1 M w j ∇ ψ r ψ ( τ ( j ) ) \begin{aligned} \nabla_\psi L(\psi)&=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ &\approx\frac{1}{N}\sum_{i=1}^N \nabla_\psi r_\psi(\tau^{(i)})-\frac{1}{\sum_jw_j}\sum_{j=1}^Mw_j\nabla_\psi r_\psi(\tau^{(j)}) \end{aligned} ∇ψ​L(ψ)​=Eτ∼π∗(τ)​[∇ψ​rψ​(τ)]−Eτ∼p(τ∣O1:T​,ψ)​[∇ψ​rψ​(τ)]≈N1​i=1∑N​∇ψ​rψ​(τ(i))−∑j​wj​1​j=1∑M​wj​∇ψ​rψ​(τ(j))​

w j = p ( τ ) e x p ( r ψ ( τ ( j ) ) ) π θ ( τ ( j ) ) = p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) e x p ( r ψ ( s t , a t ) ) p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) π θ ( a t ∣ s t ) = e x p ( ∑ t r ψ ( s t , a t ) ) ∏ t π θ ( a t ∣ s t ) \begin{aligned} w_j&=\frac{p(\tau)exp\big(r_\psi(\tau^{(j)})\big)}{\pi_\theta(\tau^{(j)})}\\ &=\frac{p(s_1)\prod_{t}p(s_{t+1}|s_t,a_t)exp(r_\psi(s_t,a_t))}{p(s_1)\prod_{t}p(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t) }\\ &=\frac{exp(\sum_tr_\psi(s_t,a_t))}{\prod_t\pi_\theta(a_t|s_t)} \end{aligned} wj​​=πθ​(τ(j))p(τ)exp(rψ​(τ(j)))​=p(s1​)∏t​p(st+1​∣st​,at​)πθ​(at​∣st​)p(s1​)∏t​p(st+1​∣st​,at​)exp(rψ​(st​,at​))​=∏t​πθ​(at​∣st​)exp(∑t​rψ​(st​,at​))​​

1. 上述過程利用另一個Policy的方式去計算了Reward Function的梯度，進而對 r ψ ( s t , a t ) r_\psi(s_t,a_t) rψ​(st​,at​)實作了更新，尋找那個reward function使專家行為産生高價值，目前行為産生低價值:

   ψ ← ψ + α ∇ ψ L ( ψ ) \psi\leftarrow\psi + \alpha \nabla_\psi L(\psi) ψ←ψ+α∇ψ​L(ψ)

2. 接下來固定目前的reward function即 r ψ ( τ ) r_\psi(\tau) rψ​(τ)，對Policy即 π θ ( a t ∣ s t ) \pi_\theta(a_t|s_t) πθ​(at​∣st​)進行REINFORCE的更新，尋找那個Policy能在目前reward下産生高價值.

   ∇ θ L ( θ ) = 1 M ∑ j = 1 M ∇ θ l o g π θ ( τ j ) r ψ ( τ j ) θ ← θ + α ∇ θ L ( θ ) \nabla_\theta L(\theta)= \frac{1}{M}\sum_{j=1}^M\nabla_\theta log\pi_\theta(\tau_j)r_\psi(\tau_j)\\ \theta \leftarrow \theta + \alpha\nabla_\theta L(\theta) ∇θ​L(θ)=M1​j=1∑M​∇θ​logπθ​(τj​)rψ​(τj​)θ←θ+α∇θ​L(θ)

3. 然後疊代更新Reward Function與Policy，其中Rewad Function往能使專家行為産生高價值同時使目前Policy行為産生低價值的方向跑，然後Policy往能在目前Reward下産生高價值的行為方向跑，進而又展現出了對抗的思想！附流程圖

三、實驗小細節

1. 專家資料從哪來？

   答: Guided Policy Search、RL from Scratch、Trajectory Optimization的Policy跑Dynamics生成出來的Trajectories

2. 如何初始化這個Policy即 π θ ( a t ∣ s t ) \pi_\theta(a_t|s_t) πθ​(at​∣st​)

   答:從random initial state開始，用Trajectory Optimization弄一個Linear-Gaussian Controller拟合專家資料或者通過Produces a motion that tracks the average demonstration with variance propor- tional to the variation between demonstrated motions

實驗結果:

四、總結

• 貢獻

  在Inverse RL的setting上，學得是一個cost function，本文利用policy update的資訊來guide cost function的學習，是以叫做Guided Cost Learning。學到一個cost function的同時，policy也學好了，隻是GAIL直接recover一個Policy而不用學習一個cost function。

• 一句話總結：不用對cost function進行人為設計，直接從raw state representation中進行Policy Optimization來指導Cost Function的Learning解決high-dimensions與Unknown Dynamics的問題
• 附錄A有對Guided Policy Search與GPS + Trajectory Optimization Under Unknown Dynamics的總結，超棒的～

啟發：此處的目标是學習一個Reward Function，利用Policy Optimization提供Guidance。優點是raw state input而不用手工對state做特征工程，但難以應對Visual input。

改進之處

1. 可以從Policy Optimization的更新上加一些Constraints，進而使Reward的指向更加明确
2. Reward更新的過程，對Partition Function采用Samples估計的方式，利用了Important Sampling，那個權重繼續可以優化，其次是逼近Partieion Functon的方式可以采用另外的方式，不一定要Samples。

Guided Cost Learning的實作代碼有點少，隻看了一份：

https://github.com/bbrighttaer/guided-irl