【資料結構&算法】14-遞歸&轉非遞歸

目錄

• 前言
• 概念定義
• 遞歸優缺點
• 遞歸條件
• 編寫遞歸代碼方法
• 遞歸思維建議
• 遞歸代碼注意翻車點
  • 堆棧溢出
  • 重複計算
• 遞歸代碼改為非遞歸代碼

前言

遞歸是一種應用非常廣泛的算法、程式設計技巧，如：

• DFS 深度優先搜尋；
• 前中後序二叉樹周遊等等。

所有的遞歸都可以轉為非遞歸實作。

李柱明部落格：https://www.cnblogs.com/lizhuming/p/15487438.html

概念定義

遞歸的定義：

• 把一個直接調用自己或者通過一系列的調用語句間接地調用自己的函數，稱為遞歸函數。
• 每個遞歸定義必須至少有一個條件，滿足時遞歸不再進行，即不再引用自身而是傳回值退出。（出口條件）

遞歸與棧結構：

• 遞歸進入時，壓棧。
• 遞歸退出時，出棧。

遞歸優缺點

優點：遞歸代碼的表達力很強，寫起來非常簡潔。

缺點：

1. 空間複雜度高。
2. 有堆棧溢出的風險。
3. 存在重複計算。
4. 過多的函數調用會耗時較多。

遞歸條件

遞歸需要滿足的兩個條件：

1. 一個問題可以分解為 n 個子問題。且子問題與原問題有着相同的形式。
   • 即是子問題和原問題相比，除了資料規模不同，其求解思路一樣。
   • 如：中序周遊二叉樹。二叉樹可以分為一個一個子樹，其求解思路都是一樣，左中右。
2. 存在遞歸終止條件。

編寫遞歸代碼方法

編寫遞歸代碼的方法 1：

1. 寫出遞推公式。
2. 找到終止條件。

如中序周遊：

1. 遞推公式，左中右：

   in_order(c) = in_order(c_left) -> print c -> in_order(c_right)

2. 終止條件：要周遊的結點為空。即是傳進來的參數為空。

例子：假如這裡有 n 個台階，每次你可以跨 1 個台階或者 2 個台階，請問走這 n 個台階有多少種走法？

分析：

• 想象成樹，下次隻能走 1 步或者走 2 步，二叉樹。
• 初步結束條件就是沒有台階了。
• 有 n 個台階的結果是左右子樹結果的和。就是

  f(n) = f(n-1) + f(n-2)

  。
• 結束條件為沒有台階，把 n 值拉到邊界進行思考。f(2) = f(1) + f(0)，剩下 2 台階時，走 1 步還剩 1 台階未結束。但是走 2 步就終止。是以固定終止條件未 f(2) = 2，f(1) = 1。

參考代碼：

int f(int n)
{
  if (n == 1) return 1;
  if (n == 2) return 2;

  return f(n-1) + f(n-2);
}
           

遞歸思維建議

編寫遞歸代碼的關鍵是，隻要遇到遞歸，我們就把它抽象成一個遞推公式，不用想一層層的調用關系，不要試圖用人腦去分解遞歸的每個步驟。

遞歸代碼注意翻車點

堆棧溢出

遞歸使用的是系統堆棧，如果系統堆棧溢出會造成系統性崩潰。

避免遞歸堆棧溢出方法：

1. 限制遞歸深度。（采用全局或者靜态變量記錄遞歸深度）

重複計算

參考上面台階例子，遞歸分解為二叉樹：

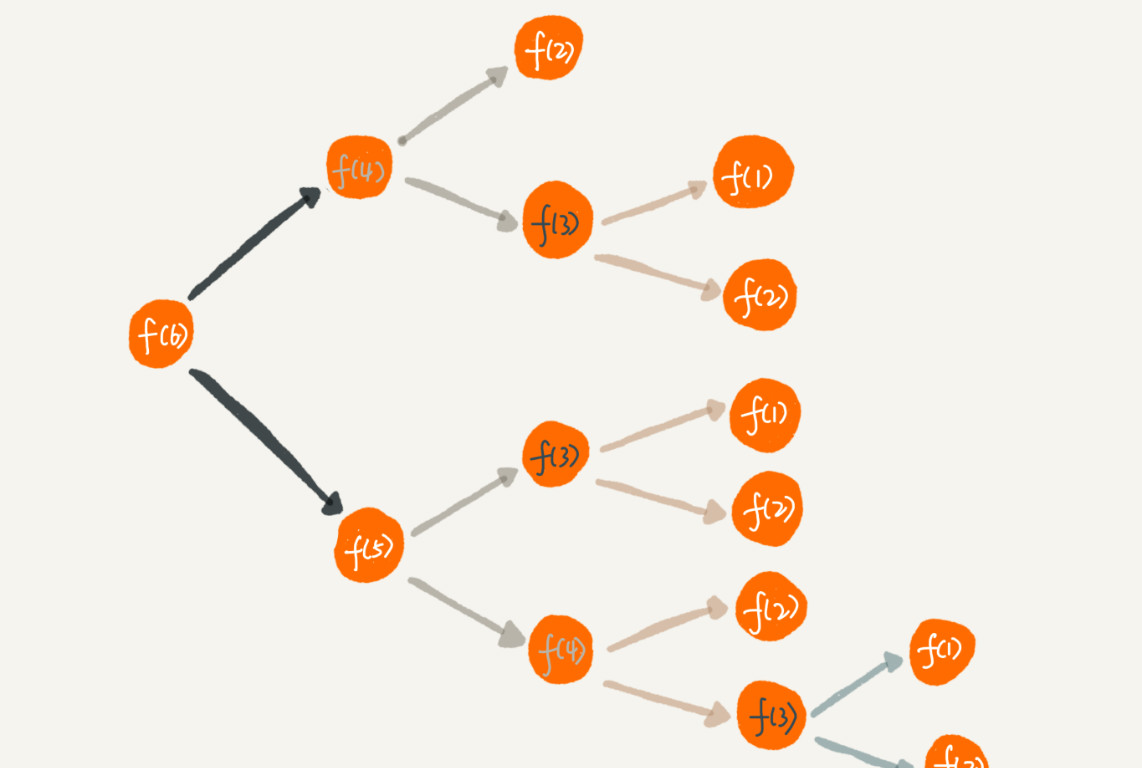
上面 f(3)就重複計算了，其實沒必要。

可以記錄每個 f(x) 的結果。在遞歸過程時優先周遊這些結果，如果沒有直接結果才計算。

儲存 f(x) 的結果的資料結構有很多種，如散清單、連結清單、樹等等。

遞歸代碼改為非遞歸代碼

所有的遞歸代碼都可以改為疊代循環的非遞歸寫法。

非遞歸方法思路：因為遞歸是借助棧來實作的，是以：

1. 遞歸中發生變化的變量（遞歸傳回值）-> 循環中每一次處理完相應變量存入 stack 中（push 進棧）。
2. 遞歸中使用遞歸傳回值 -> 循環中取出 stack 中的值進行處理（pop 出棧）。

既然入棧又出棧，那直接使用一個固定空間，如函數棧，即是使用變量來儲存該值。

一般從尾遞歸開始反過來疊代循環。意思是疊代循環是循環遞歸中出棧的流程。

如台階代碼：

• 疊代循環遞歸中出棧的部分，就是從尾遞歸開始循環，剩餘 3 步、剩餘 4 步、剩餘 5 步...的結果。
• 比如剩餘 4 步的結果是前面循環剩餘 3 步的結果和剩餘 2 步的結果之和。

int f(int n)
{
  if (n == 1) return 1;
  if (n == 2) return 2;

  int ret = 0;
  int pre = 2;
  int prepre = 1;

  for (int i = 3; i <= n; ++i)
  {
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }

  return ret;
}