一、有向無環圖
- 有方向
- 沒有閉環
二、拓撲排序
拓撲排序是将有向無環圖的頂點排成一個線性序列的過程。
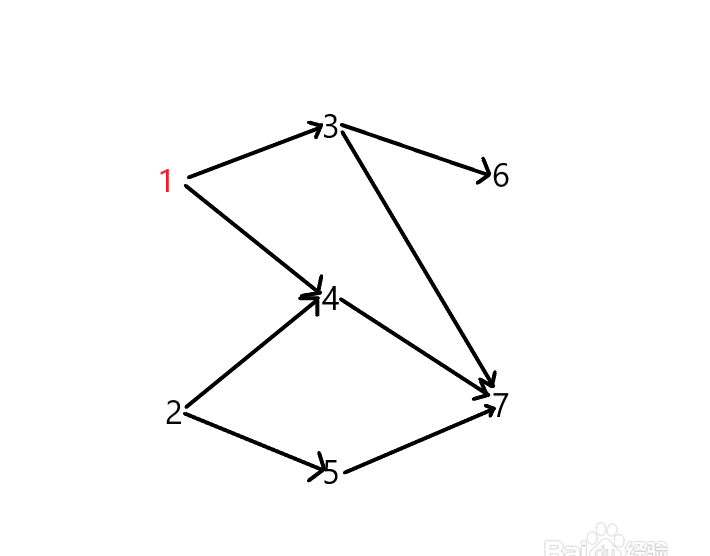
比如可将上圖
三、拓撲排序步驟
1. 首先要任意選擇一個沒有前驅的頂點,即入度為0的點,然後将它輸出。
在下面這張圖中我們選擇1為出發點。

2. 删除該節點以及與它相關聯的所有邊,這個點的nexts裡面的點入度就減少1
選擇1為出發點之後,我們将它輸出,并删除該節點以及與它相關聯的所有邊。
3. 然後在删除後的圖中繼續找一個沒有前驅的節點,
這裡沒有前驅的節點隻有2和3.
這裡我們選擇3,那麼将節點3輸出後的圖 如下圖所示。
4. 繼續找入度為0的點重複上述步驟。
接下來沒有前驅的節點隻有2和6了。
我們這裡選擇節點6,同樣的輸出節點6後删除。
然後繼續找沒有前驅的節點。這時候沒有前驅的節點隻剩下節點2.
接下來的點繼續進行拓撲排序,
5. 得到的拓撲排序的一種如下圖所示。
相信大家也都發現其實拓撲排序是不唯一的,我們選擇的出發點不同,結果就是不一樣的。
這裡給出大家針對上圖幾種拓撲排序序列。
四、算法設計
用一個map儲存他的所有節點對應的入度。
用一個隊列儲存每次入度為0的節點然後pop,pop的順序就是拓撲排序的順序。
list <node*> tsort(graph G) {
list<node*> res;
unordered_map<node*, int> inmap;
queue<node*> zeronode;
for (auto next : G.nodes) {//G.nodes是map
inmap[next.second] = next.second->in;
if (next.second->in == 0) {
zeronode.push(next.second);
}
}
while (!zeronode.empty()) {
node* cur = zeronode.front();
zeronode.pop();
res.push_back(cur);
for (auto next : cur->nexts) {
inmap[next]--;
if (inmap[next] == 0) {
zeronode.push(next);
}
}
}
return res;
}