我們已經知道了如何通過Dijkstra算法在非負權圖中找到最短路徑。即使圖中有負權邊,我們也知道通過Bellman-Ford算法找到一個從 給定的源點到其它所有節點的最短路徑。現在我們将看到一個線上性時間内運作得更快的算法,它可以在有向無環圖中找到從一個給定的源點到其它所有可達頂點的 最短路徑,又名有向無環圖(DAG)。
由于有向無環圖無環是以我們不必擔心負環的問題。正如我們已經知道在負環裡讨論最短路徑是毫無意義的一樣,因為我們可以在這些環裡不斷“循環”,但實際上我們得到的路徑将變得越來越短(構成負的環路,存在死循環)。
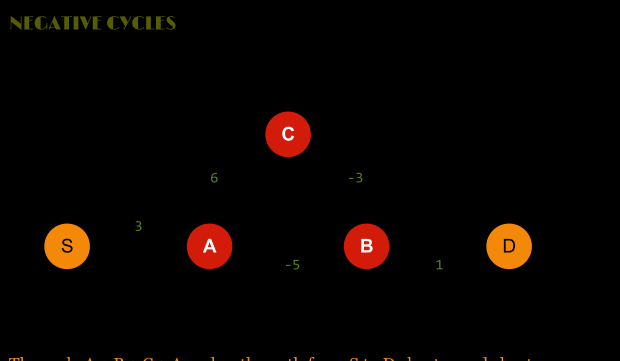
負環的存在使我們試圖找到最短路徑的行為變得毫無意義!
是以,我們要解決Dijkstra算法和的Bellman-Ford算法中的兩個問題。首先,我們隻需要非負的權重,其次,圖中不能有環。好了,這樣我們就可以通過這個算法處理滿足這兩種情況的例子了。
概述
關于有向無環圖(DAGs)我們首先要知道,它們可以很容易地進行拓撲排序。拓撲排序應用範圍非常之廣,其中最常用的或許就是用于安排依賴任務(依賴任務是同屬于一個工作中相同任務的實體,這些實體是保證互連的,它們解決共同的問題)。
拓撲排序通常是用來“排序”依賴任務的!
經過拓撲排序,我們最終會得到一張DAG圖的頂點清單,我們确信在拓撲排序清單中如果存在一條邊(u,v),那麼頂點u會先于頂點v進入清單中。
如果有一條邊(u,v),那麼頂點u一定在頂點v前面。這個結果通過這張圖檔變得更加通俗易懂。其中B和D之間沒有邊,但在清單中B在D前面!
此資訊異常重要,我們唯一需要做的事情就是通過這個排序清單來計算距離最短的路徑,這和Dijkstra算法比較相似。
好了,讓我們來總結一下這個算法:
-首先,我們必須對有向無環圖進行拓撲排序;
-其次,我們将到源點的距離初始化為0并将到其它所有頂點的距離設定為無窮大;
-最後,對于清單中的每一個頂點,我們從它的所有鄰節點中找到最短路徑的那個頂點;
這很像Dijkstra算法,但是其主要差別是我們使用了一個優先級隊列,并且此次我們使用的是經過拓撲排序的清單。
代碼
| 1 2 3 4 5 6 7 | |