一、貝葉斯定理
我們高中學過條件機率,
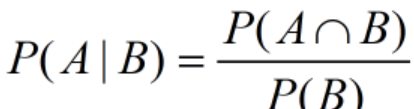
後驗機率
表示在事件B發生的情況下事件A發生的機率。
通常,事件A在事件B發生的條件下的機率,與事件B在事件A的條件下的機率是不一樣的;然而這兩者有确定的關系,貝葉斯法則就是這種關系的陳述。
貝葉斯定理表達式:
舉一個用貝葉斯公式求後驗機率的簡單例子,大家可能會很熟悉:
某射擊訓練中,射手甲的命中率是0.6,P(甲)=0.6,射手乙的命中率是0.5,P(乙)=0.5。現在甲、乙同時朝同一靶子射一槍,靶子被擊中,求甲射中的機率。
靶子被擊中P(中)有三種可能:
甲✔乙✘
甲✔乙✔
甲✘乙✔
代入貝葉斯公式我們很容易求出來:
二、樸素貝葉斯
樸素貝葉斯算法在解決資料挖掘分類問題中,用機率的形式表示資料的分類情況。屬于監督學習的生成模型,實作簡單,沒有疊代,并有堅實的數學理論作為支撐。在大量樣本下有較好的表現。
“樸素”是naïve一詞的譯意,表示在進行先驗機率計算時暗含的一個假設:事件互相條件獨立。
樸素貝葉斯問題表示如下:
我們提出假設,在ωi發生的情況下,事件互相獨立。
是以原問題轉化為條件獨立問題:
條件獨立在貝葉斯網絡中有三種形式:
1 head-to-head
指在c未知的條件下,a、b是獨立的。
例如我不知到我是否感冒的情況下,頭疼和身子沒勁兩事件并沒有直接關系,相對獨立。
2 tail-to-tail
在c 已知的情況下,a、b 獨立。
如下如,7*7的網格内部有3中基本顔色,紅(R)、黃(Y)、藍(B),三種顔色重疊的部分發生了顔色變化。
從整個網格的資料來看,R、B 不獨立。
那麼在黃色區域内部,R、B 獨立。
3 head-to-tail
經常看到報道說男人比女人更容易得肺癌,單單從實際資料上看也确實如此。但稍微結合常識考慮一下,在男人(a)和得肺癌(b)兩事件中間,還有一個十分重要的事件,吸煙(c)。男人愛抽煙,抽煙愛得肺癌。男人(a),吸煙(c),得肺癌(b)三事件就組成了一個基于head-to-tail形狀的案例。是以身為男人與得肺癌兩事件相對獨立。
三、拉普拉斯平滑
如果某類資料性狀不常出現,我們得到的資料中可能就不包含該類性狀的資料。那麼在計算樸素貝葉斯時,因為
各種機率乘在一起,一項為0整體也就為0。這對于資料分析很不利。是以我們對機率的表現形式做一點修改。拉普拉斯平滑公式如下:
公式分子分母為事件發生次數,分子+1,分母+該事件中性狀的種類。
例如,在中國男足vs南韓男足的前5場的比分是0:5,中國隊并沒有出現“赢”的性狀,那預測第六場中國隊勝出的機率為:
分母的2為輸、赢兩種性狀。
四、例子
1.拼寫檢查
我們在對單詞lunch進行搜尋時,如果不小心打成luncj或luncb,系統有時也能檢測出我們可能想輸入lunch,并搜尋單詞lunch直接給我們網頁推薦。
使用者輸入了一個單詞。這時分成兩種情況:拼寫正确,拼寫不正确。我們把拼寫正确的情況記做c(代表correct),拼寫錯誤的情況記做w(代表wrong)。
所謂"拼寫檢查",就是在發生w的情況下,試圖推斷出c。從機率論的角度看,就是已知w,然後在若幹個備選方案中,找出可能性最大的那個c,也就是求下面這個式子的最大值。
根據貝葉斯定理:
對于所有的備選的來說,對應的都是同一個w,是以它們的P(w)是相同的,是以我們求的其實是的最大值。
P(c)的含義是:某個正确的詞的出現“頻率”,它可以用“頻率”代替。如果我們有一個足夠的文本庫,那麼這個文本庫中每個單詞的出現頻率,就相當于它的發生頻率。某個詞的出現頻率越高,P(c)就越大。
的含義是:在試圖拼寫c的情況下,出現拼寫錯誤w的機率。這需要統計資料的支援,但是為了簡化問題,我們假設兩個單詞在字形上越接近,就越有可能拼錯,就越大。
舉例來說,相差一個字母的拼法,就比相差兩個字母的拼法,發生機率更高。你想拼寫單詞hello,那麼錯誤拼成hallo(相差一個字母)的可能性,就比拼成haallo高(相差兩個字母)。
是以,我們隻要找到與輸入單詞在字形上最相近的那些詞,再在其中挑出出現頻率最高的一個,就能實作的最大值。
基于上述分析,我們對拼寫檢查進行一個簡單的模拟:
建立一個小規模的文本庫。我們輸入luncj,計算目标單詞出現機率、字母數量、字母不同、字母排列等名額,求解
的最大值。
可以看到matlab輸出結果為[12;21;14;3;8],對應單詞為lunch。
2.不出門機率
下圖為某人以往14天在不同天氣狀況下是否打網球的資訊表格
今天天氣如下: