梯度下降是不同于Normal Equals的方式;梯度本質是一個試錯過程,不斷的嘗試一個個theta,尋找能夠使的成本函數值最小的可能性。所謂下降是指不斷的theat的取值是不斷小步減少的;梯度,是指這個減少是逐漸,非線性的。
梯度下降有三種常見的函數:批量梯度下降,随機梯度下降以及最小化梯度下降。
先來看批量梯度下降,在Normal Equal裡面我們接觸了函數MSE,那麼在梯度下降裡面我們還是要接觸這個MSE,但是因為theta值有多個,是以,每個theta都是一個次元,對于某個指定次元求最小值,我們對其進行求導:
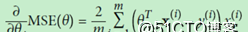
如果想要同時對多個theta求向量,可以放置到一個向量中進行,公式如下:
這樣對于多個theta的最小成本函數的求值轉變為了矩陣公式(上圖右側部分)。因為線性的成本函數是凸函數,是以我們不用安心拐點問題,隻要theta值不斷減少,cost值就會不斷減少。通常的做法是定義一個疊代的次數,即梯度的台階數,向下的每個台階都比之前的台階要小,小的程度就是上面公式的計算值;這樣擷取到的theta就是某種程度上滿足了的成本函數的最小值。
實作的python代碼如下:
theta_path_bgd = []
def plot_gradient_descent(theta, eta, theta_path=None):
m = len(X_b)
plt.plot(X, y, "b.")
n_iterations = 1000 # 定義疊代的次數
for iteration in range(n_iterations):
#為了更加直覺,前10個資料(線段)将會被列印出來
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-" if iteration > 0 else "r--"
plt.plot(X_new, y_predict, style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y) #核心的公式計算,計算下降的梯度
theta = theta - eta * gradients #theta值
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
plt.title(r"$\eta = {}$".format(eta), fontsize=16)
rnd.seed(42)
theta = rnd.randn(2,1) # random initialization
plt.figure(figsize=(10,4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.02)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
plt.show()
劃線的部分就是公式計算部分,也是整個計算過程的核心;在真實調用中,分别通過學習率0.02,0.1以及0.5進行學習,學習的效果如下圖所示,可見學習率在0.1的時候是最好的,但是在0.5則有些過,而且現象是線段在點集的上下亂竄,說明這個學習率是不可取的。0.02則學習的結果則是總在點集的下方。
批量的梯度下降已經比normal equals快很多了為什麼快?因為NE的算法中用一個矩陣的inverse(求逆矩陣),對NE算法而言将會導緻一個N*N矩陣的一次求逆矩陣的操作,非常耗時,這一點在屬性(feature)很大的時候,将會非常明顯,是以如果萬級别的,NE操作比較合适,但是超過萬級别的,梯度下降的算法将會更優,當然這個說法有待驗證。
但是每次梯度計算都是要全集計算,仍然開銷很大;有一種方法開銷非常小,而且得到的效果和全量計算差不多的,那就是随機梯度下降。他的算法就是随機抽取m個X,y值,然後根據這個X,y值來計算梯度,注意此X非彼X,隻是X全集中的一個元素,矩陣中的一列(一行),y其實隻是一個值,這樣你在來通過公式來算梯度,那可就小的多了。
Python實作如下:
theta_path_sgd = []
n_iterations = 50
t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0 / (t + t1)
m = len(X_b)
for epoch in range(n_iterations): #疊代n次(N個台階下降)
for i in range(m): #每次取m個值進行梯度下降
if epoch == 0 and i < 20:
style = "b-" if i > 0 else "r--"
random_index = rnd.randint(m)
xi = X_b[random_index:random_index+1] #取出X值,一個向量
yi = y[random_index:random_index+1] #取出y值,單個值
gradients = 2 * xi.T.dot(xi.dot(theta) - yi) #梯度值
eta = learning_schedule(epoch * m + i) #學習率,這個公式什麼用意,其實沒懂
theta = theta - eta * gradients
theta_path_sgd.append(theta)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 2, 0, 15])
theta
array([[3.90754833] ,[3.1762325 ]])
然後用ski内置的梯度下降SGDRegression來求解,注意:SGDRegression内部封裝的就是随機梯度下降的算法:
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter=50, penalty=None, eta0=0.1)
sgd_reg.fit(X, y.ravel())
sgd_reg.intercept_, sgd_reg.coef_
輸出:
(array([3.87605957]), array([3.08965292]))
基本是一樣的,SGD裡面的算法就是醬紫的(上面的上面的代碼)。
最後一種就是mini-batch,其實和随機梯度下降非常類似,隻不過SGD每次取出一個X,y,mini-batch則是每次取出一批來,差别就在這裡,下面是實作:
theta_path_mgd = []
minibatch_size = 20
t0, t1 = 10, 1000
t = 0
for epoch in range(n_iterations):
shuffled_indices = rnd.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = y[shuffled_indices]
for i in range(0, m, minibatch_size): # 周遊m次,每次增長minibatch_size
t += 1
xi = X_b_shuffled[i:i+minibatch_size]
yi = y_shuffled[i:i+minibatch_size]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)