天天看點
傳回

【軟工】第一次個人項目——數獨

一、項目源碼的github連結

https://github.com/wz111/sudoku_onlycode

（因為使用github不熟練-_-，在sudoku倉庫關聯了項目檔案夾，導緻大小接近100M。是以新開sudoku_onlycode倉庫來最終送出。為保留送出曆史，sudoku倉庫未删除）

二、需求分析

  • 生成數獨

    指令：

    sudoku.exe -c n

    要求：

    1.輸出到sudoku.txt

    2.生成的數獨不重複

    3.1<=n<=1000000，支援前置零以及前置加号，不支援運算式

    4.可以處理異常情況，如：sudoku.exe -c abc

    5.左上角第一個數為（學号後兩位相加）% 9 + 1=(8+9)%9+1=9

    6.參數不合法輸出異常資訊到控制台

  • 求解數獨

    sudoku.exe -s absolute_path_of_puzzlefile

    2.數獨中的0代表空格

    3.檔案中數獨題目數為n，1<=n<=1000000

    4.保證格式正确

    5.對每個數獨題目求出一個可行解

三、解題思路

剛拿到項目時，自然地将其分為生成終局和求解數獨兩部分。

生成終局

開始時對生成終局沒什麼思路，通過查閱資料找到這樣一篇博文，由部落客的方法以及和室友們的熱烈讨論，發現可以生成1-9中八個數的全排列，暫且将其定義為種子數組，用數組索引替換的形式，将一個已知數獨變換成另外8！-1個不同的數獨，因為[0,0]元素确定，是以是8！-1。這樣距離我們要求的1000000個數獨還有很大差距，還是經過查閱資料後，找到了一篇博文，其中介紹了基于矩陣變換的數獨生成方法，這裡我隻采用了行變換的思路，需要保證的是：交換隻發生在前三行，中間三行，最後三行之間。而不能越界交換，比如第一行和第四行交換就是不允許的。但是這種方式随機性較差，而且每次運作程式的原始矩陣都相同，是以我進行了一些改進： 在進行索引替換前，對原始的種子數組進行一次索引替換，生成一個初始種子，用這個初始種子對祖先數獨進行索引替換得到初始數獨。對這個初始數獨進行索引變換加行變換。這樣可以保證每次開始的初始數獨不一樣。

暴力回溯的想法很成熟，但是還是比較關心有沒有更好的方法，依然是查閱資料後，找到了DLX算法，即将問題轉化為精确覆寫問題求解。但是考慮到自己的水準不高，實作了DLX可能沒有時間進行充分的優化，而未優化的DLX會比暴力慢好多。思前想後還是決定寫暴力。。。在空白格的表示方法以及去除候選數的方法上，參照了這篇博文。主要想法是将數字用類似二進制的方式表示，即1=000000001,2=000000010，……， 9=100000000， 0=111111111，即每一位代表這個位置取值的可能性。取出一個數字可能性可以用取反做位與的方式，例如這個空白位置不能取2，則有111111111 & （111111101）=111111101，這樣就去除了2的可能。

四、設計實作過程

我使用了兩個類來進行資料的組織以及方法的實作。現詳細說明：

EndProducer類

  • private屬性：

int _ancestorMartix[81]： 祖先數獨

int _originalMartix[81]： 原始數獨

int _seed[9]： 原始種子數組

int _initialSeed[9]： 初始種子數組

int Nums： 要生成的數獨數量

  • public方法：
void Swap(int* a, int* b)：交換方法
int* ROWijk(int* a)：行變換方法（i,j,k的排列方式代表交換方式），傳入的是數獨數組首位址，傳回的是交換後的數組位址。
int* getInitialSeed()：得到随機的初始種子
bool DuplicateCheck(int* a, int aim, int count)：重複性檢查方法。檢查位址為a的數組中是否存在aim元素，count表示目前的數組長度。
bool IndexSubstitution(int* seed, int* a, int* b, int len)：索引替換方法。對長度為len的a數組進行以seed為種子的索引替換得到b。
void MainOperation()：主操作方法。生成數獨。

SolveSudoku類

int _puzzle[81]：數獨謎題
int _flag[81]：标記數組，如果這個位置的數是唯一的，那麼相應的标記數組位置為1，否則為0.
void setPuzzle(int a[])：顧名思義，将_puzzle指派為a
int* getPuzzle()：傳回_puzzle的副本
void setFlag(int a[])：顧名思義，将_flag指派為a
int NumTranfor(int a)：将a轉換成用到的數字。
int RemoveCandidates(int index)：去掉index位置的不合要求的候選數
bool Fill(int index)：在index位置填數

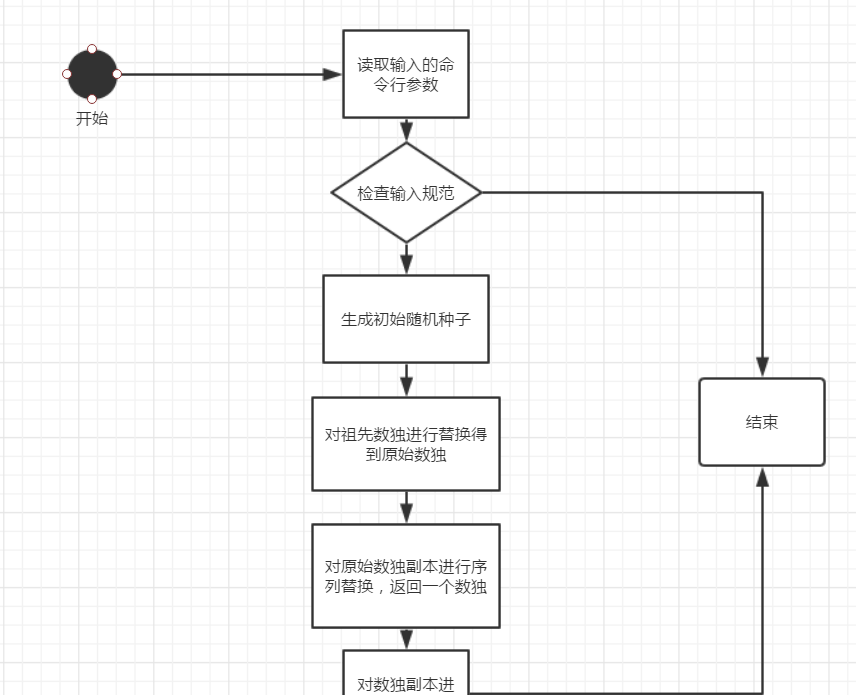
流程圖

輸入參數為'-c'：

【軟工】第一次個人項目——數獨

輸入參數為‘-s’：

【軟工】第一次個人項目——數獨

單元測試設計 

TEST_METHOD(End_Test_ROW987)
		{
			EndProducer EP(12);
			int arr[81] = { 0 };
			memset(arr + 54, 7, sizeof(int) * 9);
			memset(arr + 63, 8, sizeof(int) * 9);
			memset(arr + 72, 9, sizeof(int) * 9);
			int Real[81] = { 0 };
			memcpy(Real, EP.Row987(arr), sizeof(int) * 81);
			memset(arr + 54, 7, sizeof(int) * 9);
			memset(arr + 63, 8, sizeof(int) * 9);
			memset(arr + 72, 9, sizeof(int) * 9);
			for (int i = 54; i < 63; i++) {
				Assert::AreEqual(Real[i], arr[i + 18]);
				Assert::AreEqual(Real[i + 9], arr[i + 9]);
				Assert::AreEqual(Real[i + 18], arr[i]);
			}
		}
		TEST_METHOD(End_Test_DuplicateCheck) 
		{
			EndProducer es(12);
			int arr[10] = { 1,2,3,4,5,5,5,3,2,0 };
			int x = 6;
			int y = 1;
			int Count = 9;
			bool expect_in = es.DuplicateCheck(arr, y, Count);
			bool expect_out = es.DuplicateCheck(arr, x, Count);
			Assert::AreEqual(expect_in, true);
			Assert::AreEqual(expect_out, false);
		}
		TEST_METHOD(End_Test_getInitialSeed) 
		{
			EndProducer ep(12);
			int arr[9] = { 1,2,3,4,5,6,7,8,9 };
			int* arr1 = NULL; 
			arr1 = ep.getInitialSeed();
			for (int i = 0; i < 9; i++) {
				Assert::AreNotEqual(*(arr1 + i), arr[i]);
			}
		}
		TEST_METHOD(End_Test_IndexIndexSubstitution) 
		{
			EndProducer ep(12);
			int arr1[9] = { 4,6,3,2,1,8,9,5,7 };
			int test_seed[9] = { 9,2,4,6,5,1,7,8,3 };
			int arr2[9] = { 0 };
			ep.IndexSubstitution(test_seed, arr1, arr2, 9);
			int expect_arr2[9] = { 6,1,4,2,9,8,3,5,7 };
			for (int i = 0; i < 9; i++) {
				Assert::AreEqual(arr2[i], expect_arr2[i]);
			}
		}
		TEST_METHOD(Sol_Test_setPuzzle) 
		{
			SolveSudoku test_ss;
			int x[81] = { 0 };
			x[1] = 9;
			x[5] = 1;
			x[4] = 2;
			test_ss.setPuzzle(x);
			int* y = test_ss.getPuzzle();
			Assert::AreEqual(x[1], y[1]);
			Assert::AreEqual(x[4], y[4]);
			Assert::AreEqual(x[5], y[5]);
		}
		TEST_METHOD(Sol_Test_NumTransfor)
		{
			SolveSudoku test_ss;
			int x1 = 1;
			int x2 = 4;
			int x3 = 9;
			Assert::AreEqual(test_ss.NumTransfor(x1), 0x1);
			Assert::AreEqual(test_ss.NumTransfor(x2), 0x8);
			Assert::AreEqual(test_ss.NumTransfor(x3), 0x100);
		}

關于單元測試，我是對每個類中的每個方法單獨進行了進行了測試，具體代碼可參看頂部的github連結。

【軟工】第一次個人項目——數獨

覆寫率

這是參數為‘-c’時EndProducer類的覆寫率：

【軟工】第一次個人項目——數獨

這是參數為‘-s’時SolveSudoku類的覆寫率：

【軟工】第一次個人項目——數獨

五、性能分析

最開始的版本生成1000000個數獨需要263秒左右的時間，啟動性能分析，檢視生成數獨部分的調用關系樹

【軟工】第一次個人項目——數獨

發現開銷最大的函數是這個out<<，找到這部分的代碼，發現我們是每次向檔案中輸出一個字元，又因為c++中IO會占用較長時間

是以改用fputs，一次輸出一個終盤。修改後的時間達到了3.76s。

【軟工】第一次個人項目——數獨

解題方面，性能分析發現開銷最大的函數是Fill(int index)，意料之中。而且RemoveCandidates方法以及NumTransfor方法均在Fill中被調用，才造成開銷大的問題。

【軟工】第一次個人項目——數獨

六、代碼分析

行變換函數，僅以978變換為例

int* EndProducer::Row978(int* a)
{
	int top = (7 - 1)*NUM_ROW;
	int end = (9 - 1)*NUM_ROW;

	for (int i = 0; i < NUM_ROW; i++) {
		Swap(&a[top + i], &a[end + i]);
	}
	top = (8 - 1)*NUM_ROW;
	end = (9 - 1)*NUM_ROW;

	for (int i = 0; i < NUM_ROW; i++) {
		Swap(&a[top + i], &a[end + i]);
	}
	return a;
}

索引替換方法

void EndProducer::IndexSubstitution(int* seed, int* a, int* b, int len)
{    
	int i;
	//int result[81] = { 0 };
        for( i = 0 ; i < len ; i++ )
	{
		int temp = a[i];
		b[i] = seed[temp - 1];
	}
}

謎題數字轉換，其中NUM1~NUM9均在頭檔案中定義

int SolveSudoku::NumTransfor(int a) 
{
	int temp = 0;
	switch (a)
	{
	case 1:
		temp = NUM1;
		break;
	case 2:
		temp = NUM2;
		break;
	case 3:
		temp = NUM3;
		break;
	case 4:
		temp = NUM4;
		break;
	case 5:
		temp = NUM5;
		break;
	case 6:
		temp = NUM6;
		break;
	case 7:
		temp = NUM7;
		break;
	case 8:
		temp = NUM8;
		break;
	case 9:
		temp = NUM9;
		break;
	default:
		cout << "Error4" << endl;
		exit(1);
		break;
	}
	return temp;
}

去除index位置中不符合要求的候選數。

int SolveSudoku::RemoveCandidates(int index) 
{
	if (_flag[index] == 1)
	{
		return _puzzle[index];
	}

	int row = index / 9;
	int col = index % 9;
	int m = row / 3;
	int n = col / 3;
	int i1;
	int j1;
	int pointCopy = _puzzle[index];

	//Palace candidates removal
	for (i1 = m * 3; i1 < m * 3 + 3; i1++)
	{
		for (j1 = n * 3; j1 < n * 3 + 3; j1++)
		{
			if (_flag[i1 * 9 + j1] == 1) 
			{
				pointCopy = pointCopy & (~NumTransfor(_puzzle[i1 * 9 + j1]));
			}
		}
	}

    //row and col candidates removal
	int i;
	for (i = 0; i < 9; i++) 
	{
		if (_flag[row * 9 + i] == 1) 
		{
			pointCopy = pointCopy & (~NumTransfor(_puzzle[row * 9 + i]));
		}
		if(_flag[i * 9 + col] == 1)
		{
		    pointCopy = pointCopy & (~NumTransfor(_puzzle[i * 9 + col]));
		}
		else
			;
	}
	return  pointCopy;
}

回溯求解數獨的Fill方法

bool SolveSudoku::Fill(int index) 
{	
	if (index >= 81) 
	{
		return true;
	}
	int shiftvalue = RemoveCandidates(index);
	int pointCopy = _puzzle[index];
	
	if(_flag[index] == 0)
	{
		for (int i = 1 ; shiftvalue > 0 ; i++) 
		{
			if (shiftvalue % 2 != 0)
			{
				_puzzle[index] = i;
				_flag[index] = 1;
				if (Fill(index + 1))
				{
					return true;
				}
			}
			shiftvalue = shiftvalue >> 1;
		}
	}
	else
	{
		return Fill(index + 1);
	}
	_puzzle[index] = pointCopy;
	_flag[index] = 0;
	return false;
}

七、PSP圖

【軟工】第一次個人項目——數獨

八、總結

這次作業應該是我第一次文檔指揮編碼的作業，結果還是不太成功，實作過程中還是出現了該文檔的問題，由此暴露出的問題有幾個。

一個是對C++不熟悉，以至于編碼前先去看了幾節C++面向對象的網課，但感覺效果不好，還不如在編碼過程中學到的多。

還有就是這次太重視設計了，以至于有時候想的偏離了正确軌道，意識到的時候發現和項目好像沒啥關系。

最後還是C的基礎不紮實，經常會寫着寫着去查百度，很多知識沒有熟練掌握，這大幅增加了編碼時間。

2017.9.29修改

  • 将Rowjik方法進行了整合，修改為RowSwap函數，github已更新。主要思路為将目标序列與升序序列比較，若相對位置不同，則替換兩者所對應行，同時替換兩者位置，直到與升序序列相等時停止。
  • 今天看到作業結果居然生成了重複的終局，心态炸穿，在EndProducer.cpp中的MainOperation函數中發現了問題，是個老生常談的錯誤了，因為我的行變換函數是直接修改位址，是以在對原始矩陣進行變換的時候要保留一個副本，我想到了這個問題，實作的時候卻犯了想當然的錯誤！我建立了一個int* OriMartixCopy來保留副本，同時建立了一個int* OriMarRowCopy來用于行變換，結果在指派時直接寫成了： 
OriMarRowCopy = OriMartixCopy;

相當于将兩個指針同時指向原數組，失去了原本的意義。現在改為：

for(int i = 0 ; i < 81 ; i++)
{
        OriMarRowCopy[i] = OriMartixCopy[i];
}

相應的，單元測試也進行了修改。但是在解題時居然會題目與解的數目不一，有些費解，以後再查。

  • 這個問題也已經找到，還是對C++流處理的了解不夠，寫入出現問題： 
fstream outfile("sudoku.txt");

初步試驗後發現，寫成ofstream就可以，

ofstream outfile("sudoku.txt");

查閱了C++ Reference關于fstream和ofstream的内容後發現，fstream有一個成員常數out，這個out會使内部緩沖流支援檔案寫入操作，而在ofstream中，這個out是預設設定的。是以ofstream可以而fstream不行，也可以在構造時對fstream進行手動添加成員常量out，即：

fstream outfile("sudoku.txt", std::fstream::out);

總結一下，還是懶，其實花少量的時間寫一個測試程式就可以解決的。這次就引以為戒，在結對項目中絕對絕對不能這麼馬虎了。

軟體工程
上一篇: [2017BUAA軟工]個人項目
下一篇: 2017BUAA軟工個人作業Week1

繼續閱讀