LCA(Lowest Common Ancestor 最近公共祖先)定義如下:在一棵樹中兩個節點的LCA為這兩個節點所有的公共祖先中深度最大的節點。
比如這棵樹
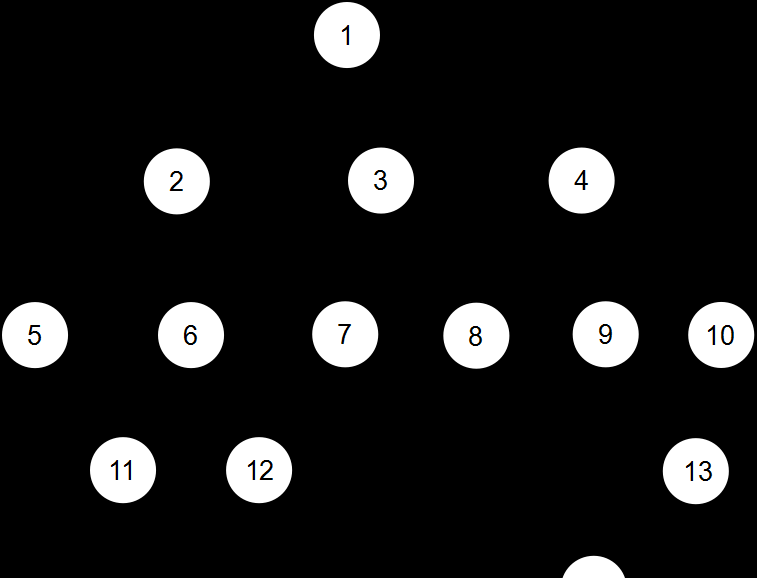
結點5和6的LCA是2,12和7的LCA是1,8和14的LCA是4。
這裡講一下用樹鍊剖分來求LCA。
先想一下,若要求結點13和4的LCA,那很顯然是4,因為他們在一條重鍊上。所謂的重鍊,就是取每個結點u的所有子節點中,子樹最大的子結點v,然後将邊(u,v)作為重邊,其餘邊作為輕邊,重邊構成的鍊就是重鍊。子樹最大就是指該點所得孩子結點最多(這裡要包括他自己)。
我們先找出所有的重鍊。
可見這棵樹有7條重鍊(包括一條鍊隻有一個結點的)。每一條重鍊的頂點就是該鍊上深度最小的結點。
而樹鍊剖分的目标就是将要求的兩個點轉換到一條重鍊上,這樣LCA就是該條重鍊上深度較小的結點了。
具體實作步驟拿第一幅圖中的結點12和14舉例。首先要比較的是12和14所在鍊的頂點的深度,可見12所在鍊的頂點更深,此時将12跳到它的頂點12的父親結點6。然後再比較6所在鍊的頂點和14所在鍊的頂點,循環下去直到兩個點到同一個鍊上,最後比較,收尾。
這就是樹鍊剖分的基本思想了,那我就開始寫了。
首先跑兩遍dfs,第一遍是建樹和建鍊,第二遍是記錄每一個結點的頂點(這樣就知道該點所在鍊的頂點的深度了)。然後就是用上述思想求LCA。
我們以洛谷的闆子為例,傳送門:https://www.luogu.org/problemnew/show/P3379
上代碼(懶得用鄰接表存圖了,上vector)
其中vis數組是為了解決無向圖存兩次邊的問題。
1 #include<cstdio>
2 #include<iostream>
3 #include<cmath>
4 #include<algorithm>
5 #include<cstring>
6 #include<vector>
7 using namespace std;
8 const int maxn = 5e5 + 5;
9 vector<int>v[maxn];
10 /*第一遍dfs主要來維護以下這些數組,size[now]指結點now的子樹大小,dep[now]指結點now的深度,
11 Maxson[now]指now所在鍊上結點now的下一個結點(用來建鍊) */
12 int vis[maxn], size[maxn], dep[maxn], fa[maxn], Maxson[maxn];
13 void dfs1(int now)
14 {
15 vis[now] = 1; size[now]= 1;
16 for(int i = 0; i < v[now].size(); ++i)
17 if(!vis[v[now][i]])
18 {
19 dep[v[now][i]] = dep[now] + 1;
20 fa[v[now][i]] = now;
21 dfs1(v[now][i]);
22 size[now] += size[v[now][i]]; //結點now的子樹大小就是他所有孩子結點的大小之和加1(包括自己)
23 if(size[v[now][i]] > size[Maxson[now]]) Maxson[now] = v[now][i]; //選重邊
24 }
25 }
26 int path[maxn];
27 void dfs2(int now)
28 {
29 vis[now] = 1;
30 for(int i = 0; i < v[now].size(); ++i)
31 if(!vis[v[now][i]])
32 {
33 if(Maxson[now] == v[now][i]) path[v[now][i]] = path[now];
34 else path[v[now][i]] = v[now][i]; //新開辟一條鍊
35 dfs2(v[now][i]);
36 }
37 }
38 int lca(int x, int y)
39 {
40 while(path[x] != path[y]) //若不在一條鍊上
41 {
42 if(dep[path[x]] > dep[path[y]]) x = fa[path[x]];
43 else y = fa[path[y]];
44 }
45 return dep[x] < dep[y] ? x : y;
46 }
47 int main()
48 {
49 int n, m, s; scanf("%d%d%d", &n, &m, &s);
50 for(int i = 1; i < n; ++i)
51 {
52 int a, b; scanf("%d%d", &a, &b);
53 v[a].push_back(b); v[b].push_back(a);
54 }
55 dep[s] = 0; memset(vis, 0, sizeof(vis));
56 dfs1(s);
57 path[s] = s; memset(vis, 0, sizeof(vis));
58 dfs2(s);
59 for(int i = 1; i <= m; ++i)
60 {
61 int a, b; scanf("%d%d", &a, &b);
62 printf("%d\n", lca(a, b));
63 }
64 return 0;
65 }