前面主要介紹了AVL的基本概念與結構,下面開始詳細介紹AVL的實作細節;
AVL樹實作的關鍵點
AVL樹與二叉搜尋樹結構類似,但又有些細微的差別,從上面AVL樹的介紹我們知道它需要維護其左右節點平衡,實作AVL樹關鍵在于标注節點高度、計算平衡因子、維護左右子樹平衡這三點,下面分别介紹;
标注節點高度
從上面AVL樹的定義中我們知道AVL樹其左右節點高度差不能超過一,是以我們需要标注出每個節點高度;
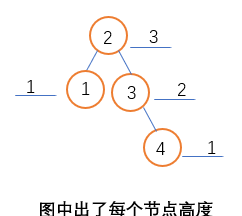
1、節點高度為最大的子節點高度加1,其中葉子節點高度為1;
2、1與4葉子節點高度為1,節點3高度為節點4的高度加1,節點2高度為1與3節點中最大的高度加1;
3、節點初始化時高度為1,當在AVL中添加與删除節點時需要維護其節點高度,在AVL添加節點後需要重新計算目前添加節點的高度;
計算平衡因子
标注了每個節點高度後此時可以輕松算出每個節點的平衡因子,隻需其節點左子樹與右子樹的高度差的絕對值即可;
1、1、4葉子節:平衡因子為0
2、節點3:右子樹高度為1,左子樹其高度為0,0-1絕對值為1,此節點平衡因子為1
3、節點2:左子樹高度為1,右子樹高度為2,1-2絕對值為1,此節點平衡因子為1
維護左右子樹平衡
當在AVL中添加與删除節點時都可能造成AVL變成失去平衡狀态使之退化為二叉搜尋樹,AVL中主要在添加節點與删除節點時需要維護其左右子樹的平衡因子;
添加節點
添加節點最終都是添加到葉子節點上,節點添加後其先祖節點可能出現了失去平衡的情況,需要從添加的節點開始向上維護平衡性,向上查找不平衡節點;
右旋轉
新增節點在不平衡節點左側的左側,同時不平衡節點左子樹高度大于等于右子樹高度(左子樹平衡因子大于等于右子樹平衡因子);
添加節點1後第一個不平衡節點為節點3,同時節點3左子樹高度大于右子樹高度,此時需要不平衡節點向右旋轉;
通過如下操作完成節點右旋轉;
T = 2.right
2.right = 3
3.left = T
左旋轉
新增節點在不平衡節點右側的右側,同時不平衡節點右子樹高度大于等于左子樹高度(右子樹平衡因子大于等于左子樹平衡因子);
添加節點3後,節點1失去平衡 添加節點3後第一個不平衡節點為節點1,同時節點1右子樹高度大于左子樹高度,此時需要不平衡節點向左旋轉;
通過如下操作完成節點左旋轉;
T = 2.left
2.left = 1
1.right = T
先左旋轉後右旋轉
新增節點在不平衡節點左側的右側
先左旋轉,變成了右旋轉問題,重複上面說所的右旋轉;
T = 4.left
Y = T.right
Z = Y.left
Y.left = T
T.right = Z
4.left = Y
先右旋轉後左旋轉
新增節點在不平衡節點右側的左側
先右旋轉,變成了左旋轉問題,重複上面說所的左旋轉;
T = 2.right
Y = T.left
Z = Y.right
Y.right = T
T.left = Z
2.right = Y
删除節點
删除節點是AVL樹也可能會失去平衡,是以也需要維護AVL的平衡性;
節點的删除右這麼幾個步驟:
1、 要删除的節點比目前節點小時在左子樹查找
2、 要删除的節點比目前節點大時在右子樹查找
3、 要删除節點為目前節點且左子樹為空時右子樹頂上
4、 要删除節點為目前節點且右子樹為空時左子樹頂上
5、 要删除節點左右子樹均存在時,大于目前節點的最小節點頂上
6、 更新節點高度值
7、 計算節點平衡因子
8、 進行與添加節點時一樣的平衡因子維護操作
文章首發位址:Solinx
http://www.solinx.co/archives/1330