布隆過濾器原理
布隆過濾器有什麼用?
布隆過濾器是可以用于判斷一個元素是不是在一個集合裡,并且相比于其它的資料結構,布隆過濾器在空間和時間方面都有巨大的優勢。
特點:
- 巴頓.布隆于一九七零年提出
- 一個很長的二進制向量 (位數組)
- 一系列随機函數 (哈希)
- 空間效率和查詢效率高:O(1)
- 有一定的誤判率(哈希表是精确比對)
實作原理
布隆過濾器(Bloom Filter)的核心實作是一個超大的位數組和幾個哈希函數。假設位數組的長度為m,哈希函數的個數為k
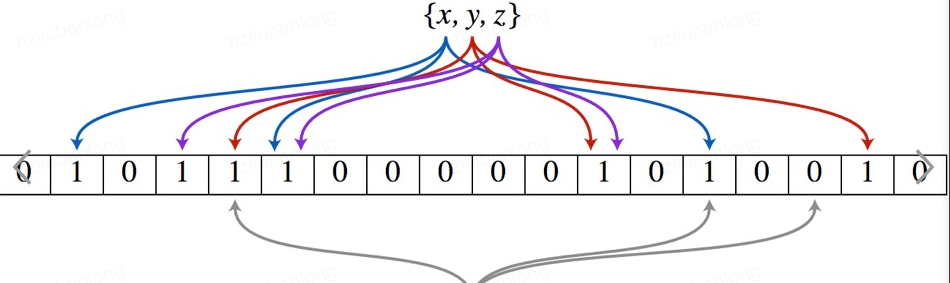
以上圖為例,具體的操作流程:假設集合裡面有3個元素{x, y, z},哈希函數的個數為3(這裡元素個數和哈希函數的數量沒有直接關系)。
首先将位數組進行初始化,将裡面每個位都設定位0。
對于集合裡面的每一個元素,将元素依次通過3個哈希函數進行映射,每次映射都會産生一個哈希值,這個值對應位數組上面的一個點,然後将位數組對應的位置标記為1。
查詢W元素是否存在集合中的時候,同樣的方法将W通過哈希映射到位數組上的3個點。如果3個點的其中有一個點不為1,則可以判斷該元素==一定==不存在集合中。反之,如果3個點都為1,則該元素==可能==存在集合中。
注意:此處不能判斷該元素是否一定存在集合中,可能存在一定的==誤判率==。可以從圖中可以看到:假設某個元素通過映射對應下标為4,5,6這3個點。雖然這3個點都為1,但是很明顯這3個點是不同元素經過哈希得到的位置,是以這種情況說明元素雖然不在集合中,也可能對應的都是1,這是誤判率存在的原因。
java代碼實作
可以看下面這段代碼,也可以到
https://archive.codeplex.com/?p=bloomfilter這個位址看開源代碼
import java.io.Serializable;
import java.util.BitSet;
import java.util.concurrent.atomic.AtomicInteger;
public class BloomFileter implements Serializable {
private static final long serialVersionUID = -5221305273707291280L;
private final int[] seeds;
private final int size;
private final BitSet notebook;
private final MisjudgmentRate rate;
private final AtomicInteger useCount = new AtomicInteger(0);
private final Double autoClearRate;
/**
* 預設中等程式的誤判率:MisjudgmentRate.MIDDLE 以及不自動清空資料(性能會有少許提升)
*
* @param dataCount 預期處理的資料規模,如預期用于處理1百萬資料的查重,這裡則填寫1000000
*/
public BloomFileter(int dataCount) {
this(MisjudgmentRate.MIDDLE, dataCount, null);
}
/**
* @param rate 一個枚舉類型的誤判率
* @param dataCount 預期處理的資料規模,如預期用于處理1百萬資料的查重,這裡則填寫1000000
* @param autoClearRate 自動清空過濾器内部資訊的使用比率,傳null則表示不會自動清理,
* 當過濾器使用率達到100%時,則無論傳入什麼資料,都會認為在資料已經存在了
* 當希望過濾器使用率達到80%時自動清空重新使用,則傳入0.8
*/
public BloomFileter(MisjudgmentRate rate, int dataCount, Double autoClearRate) {
long bitSize = rate.seeds.length * dataCount;
if (bitSize < 0 || bitSize > Integer.MAX_VALUE) {
throw new RuntimeException("位數太大溢出了,請降低誤判率或者降低資料大小");
}
this.rate = rate;
seeds = rate.seeds;
size = (int) bitSize;
notebook = new BitSet(size);
this.autoClearRate = autoClearRate;
}
public void add(String data) {
checkNeedClear();
for (int i = 0; i < seeds.length; i++) {
int index = hash(data, seeds[i]);
setTrue(index);
}
}
/**
* 如果不存在就進行記錄并傳回false,如果存在了就傳回true
*
* @param data
* @return
*/
public boolean addIfNotExist(String data) {
checkNeedClear();
int[] indexs = new int[seeds.length];
// 先假定存在
boolean exist = true;
int index;
for (int i = 0; i < seeds.length; i++) {
indexs[i] = index = hash(data, seeds[i]);
if (exist) {
if (!notebook.get(index)) {
// 隻要有一個不存在,就可以認為整個字元串都是第一次出現的
exist = false;
// 補充之前的資訊
for (int j = 0; j <= i; j++) {
setTrue(indexs[j]);
}
}
} else {
setTrue(index);
}
}
return exist;
}
private void checkNeedClear() {
if (autoClearRate != null) {
if (getUseRate() >= autoClearRate) {
synchronized (this) {
if (getUseRate() >= autoClearRate) {
notebook.clear();
useCount.set(0);
}
}
}
}
}
public void setTrue(int index) {
useCount.incrementAndGet();
notebook.set(index, true);
}
private int hash(String data, int seeds) {
char[] value = data.toCharArray();
int hash = 0;
if (value.length > 0) {
for (int i = 0; i < value.length; i++) {
hash = i * hash + value[i];
}
}
hash = hash * seeds % size;
// 防止溢出變成負數
return Math.abs(hash);
}
public double getUseRate() {
return (double) useCount.intValue() / (double) size;
}
/**
* 配置設定的位數越多,誤判率越低但是越占記憶體
* <p>
* 4個位誤判率大概是0.14689159766308
* <p>
* 8個位誤判率大概是0.02157714146322
* <p>
* 16個位誤判率大概是0.00046557303372
* <p>
* 32個位誤判率大概是0.00000021167340
*
* @author lianghaohui
*/
public enum MisjudgmentRate {
// 這裡要選取質數,能很好的降低錯誤率
/**
* 每個字元串配置設定4個位
*/
VERY_SMALL(new int[]{2, 3, 5, 7}),
/**
* 每個字元串配置設定8個位
*/
SMALL(new int[]{2, 3, 5, 7, 11, 13, 17, 19}), //
/**
* 每個字元串配置設定16個位
*/
MIDDLE(new int[]{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53}), //
/**
* 每個字元串配置設定32個位
*/
HIGH(new int[]{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
101, 103, 107, 109, 113, 127, 131});
private int[] seeds;
private MisjudgmentRate(int[] seeds) {
this.seeds = seeds;
}
public int[] getSeeds() {
return seeds;
}
public void setSeeds(int[] seeds) {
this.seeds = seeds;
}
}
public static void main(String[] args) {
BloomFileter fileter = new BloomFileter(7);
System.out.println(fileter.addIfNotExist("1111111111111"));
System.out.println(fileter.addIfNotExist("2222222222222222"));
System.out.println(fileter.addIfNotExist("3333333333333333"));
System.out.println(fileter.addIfNotExist("444444444444444"));
System.out.println(fileter.addIfNotExist("5555555555555"));
System.out.println(fileter.addIfNotExist("6666666666666"));
System.out.println(fileter.addIfNotExist("1111111111111"));
}
} 錯誤率估算
純數學算法推導,公式參見:布隆過濾器 (Bloom Filter) 詳解
下面給出一個直覺的圖:
- m:存儲比特位的數組長度(數組長度越長,元素越小,則誤判幾率越低)注意:m必須>n,不然當隻有一個哈希函數的時候都一定會出現hash沖突
- n:需要存儲轉換的元素的個數
- K:把元素M映射在數組上哪一位為1的哈希函數的個數。 K要 <= m/n