計算機組成原理第二章資料的表示和運算

第二章資料的表示和運算

數制與編碼

進制轉換

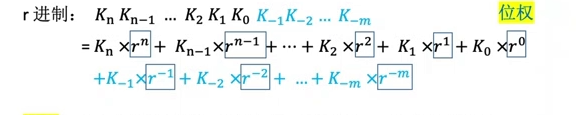
使用二進制的原因

二進制與八進制、十六進制的轉換

各種進制的書寫方式

十進制轉換為任意進制

整數部分

\[\begin{align}

&十進制轉換二進制\\

&如(75)_{10}\\

&\frac{75}{2}=37……1\space K_0\\

&\frac{37}{2}=18……1\space K_1\\

&\frac{18}{2}=9……0\space K_2\\

&\frac{9}{2}=4……1\space K_3\\

&\frac{4}{2}=2……0\space K_4\\

&\frac{2}{2}=1……0\space K_5\\

&\frac{1}{2}=0……1\space K_6\\

&K_0K_1K_2K_3K_4K_5K_6=1101001

\end{align}

小數部分

&如(75.3)_{10} \space\space小數部分=0.3\\

&0.3*2=0.6=0+0.6 \space K_{-1}\\

&0.6*2=1.2=1+0.2 \space K_{-2}\\

&0.2*2=0.4=0+0.4 \space K_{-3}\\

&0.4*2=0.8=0+0.8 \space K_{-4}\\

&0.8*2=1.6=1+0.6 \space K_{-5}\\

&……\\

&0.3D=0.01001……B\\

&小數無法準确表述\\

十進制轉換二進制（拼湊法）

總結

BCD碼（Binary-Coded Decimal）

修正資料

&(9+9)_{10}\\

&(9)_{10}\rightarrow (1001)_2\\

&(9+9)_{2}=1001 1001\\

&1001\\

+&1001\\

-&---\\

1&0010\\

&10010超出了8421碼中的1010-1111\\

&+(6)_{10}\Leftrightarrow+(0110)_2修正\\

+&0110\\

1&1000\\

相加結果在合法範圍(1010~1111)内，不需要修正

其他編碼

字元與字元串

ASCII碼

可印刷字元：32~126

其餘為控制、通信字元

大寫字母：65（0100 0001）~ 90（0101 1010）

小寫字母：97（0110 0001）~ 122（0111 1010）

漢字的表示和編碼

輸入：輸入編碼

輸出：漢字字形碼

字元串

大端模式&小端模式

奇偶校驗碼

校驗原理

&當d=1時，無檢錯能力；當d=2時，有檢錯能力；當d\geq3時，若設計合理，可能具有檢錯糾錯能力（海明碼）\\

例題

&奇校驗：(1)1001101~~(0)1010111\\

&偶校驗：(0)1001101~~(1)1010111\\

隻能發現資料代碼中奇數位的出錯情況，但不能糾錯

海明碼

簡單思路

求解步驟

循環備援校驗碼

基本思想

校驗步驟（模二除）

&G(x)=x^3+x^2+1=1*x^3+1*x^2+0*x^1+1*x^0\rightarrow 1101\\

&~~~~~~110101\\

&-------------------\\

1101~|&101001000\\

&1101\\

&~~1110\\

&~~1101\\

&~~~~0111\\

&~~~~0000\\

&~~~~~~1110\\

&~~~~~~1101\\

&~~~~~~~~0110\\

&~~~~~~~~0000\\

&~~~~~~~~~~1100\\

&~~~~~~~~~~1101\\

&~~~~~~~~~~~~001\rightarrow校驗位\\

&對應的CRC碼為101001~~001

餘數為001、010時并不能确定是哪一位出錯了

此時是資訊位過多，降低資訊位就可以解決問題

&K個資訊位，R個校驗位，若生成多項式選擇得當，且2^R\geq K+R+1，則CRC碼可糾正1位錯\\

定點數的表示

無符号數

通常隻有無符号整數，而沒有無符号小數

&1001100B\\

&=1*2^7+1*2^6+0*2^5+0*2^4+1*2^3+1*2^2+0*2^1+0*2^0\\

&=156D\\

有符号數的定點表示

原碼

用尾數表示真值部分的絕對值，符号位“0/1”對應“正/負”

若機器字長為n+1位，則尾數占n位

反碼

若符号位為0，則反碼與原碼相同

若符号位為1，則數值位全部取反

反碼是原碼轉變為補碼的一個中間狀态

補碼

正數的補碼=原碼

負數的補碼=反碼末位+1（要考慮進位）

&設機器字長為8位\\

&[+0]_{原}=0000~0000\\

&[+0]_{反}=0000~0000\\

&[+0]_{補}=0000~0000\\

&\\

&[-0]_{原}=1000~0000\\

&[-0]_{反}=1111~1111\\

&[-0]_{補}=1~0000~0000\\

&由于機器字長為8位，進位丢棄\\

&[-0]_{補}=0000~0000\\

逆向

将負數補碼轉回原碼的方法相同：尾數取反，末尾+1

&[-19]_{原}=1001~0011\\

&[-19]_{反}=1110~1100\\

&[-19]_{補}=1110~1101\\

&[-19]_{原}=1001~0010+0000~0001=1001~0011\\

移碼

補碼的基礎上将符号位取反

移碼隻能用于表示整數

幾種碼表示定點整數

練習

&假設機器字長為8位\\

&定點整數x=50\\

&[+50]_{原}=0011~0010\\

&[+50]_{反}=0011~0010\\

&[+50]_{補}=0011~0010\\

&[+50]_{移}=1011~0010\\

&定點整數x=-100\\

&[-100]_{原}=1110~0100\\

&[-100]_{反}=1001~1011\\

&[-100]_{補}=1001~1100\\

&[-100]_{移}=0001~1110\\

知識回顧

各種碼的作用

用加法代替減法

表盤為例

&10+9=19\\

&19\%12=7\\

&相當于求餘數\\

模運算的性質

可以說在模12的情況下上述數字等價

其中-3和9互為補數，二者絕對值之和等于模

有符号數&~~~~~~~~~~~~~~~~~~~無符号數\\

14~~~~~~&0000~1110~~~~~~~~14\\

-14~~~+&1000~1110~~~~~~142\\

-----&-----------\\

0~~~~~~&1001~1100~~~~~~156\\

&模-a的絕對值=a的補數\\

&0000~1110\\

-&0000~1110\\

&0000~0000\\

&模2^8-0000~1110\\

&1~0000~0000\\

-&~~~0000~1110\\

&~~~1111~0010\\

&~~~0000~1110\\

+&~~~1111~0010\\

&~1~0000~0000\\

&求-66的補碼\\

&[-66]_{原}=1100~0010\\

&[-66]_{反}=1011~1101\\

&[-66]_{補}=1011~1110\\

&[+88]_{原}=0101~1000\\

&1101~1000\\

+&0011~1110\\

--&-----------------\\

1~&0001~0110~~~~~~22D\\

移位運算

算術移位

原碼的算術移位

&[+20]_{原}=0001~0100\\

&{左移一位}=0010~1000=+40D\\

反碼的算數移位

補碼的算數移位

&[-20]_{原}=1001~0100\\

&[-20]_{反}=1110~1011\\

&[-20]_{補}=1110~1100\\

&左移一位=1010~1000\\

&右移一位=1111~0110\\

邏輯移位（針對無符号數）

應用舉例

循環移位

加減運算

原碼的加減運算

補碼的加減運算

&A=15,B=-24,C=124,求[A+C]_{補}[B-C]_{補}\\

&[A]_{原}=0000~1111\\

&[A]_{反}=0000~1111\\

&[A]_{補}=0000~1111\\

&[B]_{原}=1001~1000\\

&[B]_{反}=1110~0111\\

&[B]_{補}=1110~1000\\

&[C]_{原}=0111~1100\\

&[C]_{反}=0111~1100\\

&[C]_{補}=0111~1100\\

&[A+C]_{補}\\

&0000~1111\\

+&0111~1100\\

----&------------\\

&1000~1011\\

&1111~0100\\

&1111~0101~~~~~~-117D\\

&[B-C]_{補}\\

1&~0000~0000\\

-&~0111~1100\\

----&-------------\\

&~1000~0100\\

+&~1110~1000\\

&~0110~1100\\

&~0110~1100~~~~~~+108D\\

出現了溢出

溢出判斷

一位符号邏輯表達式

進位判斷

雙符号位

符号擴充

整數

小數

乘法運算

手算乘法（十進制）

手算乘法（二進制）

原碼一位乘法

實作方法：先加法再移位，重複n次

（0）乘法進行前ACC置0

（1）第一步加法

加法

移位

（2）第二步加法

（3）第三步加法

（4）第四步加法

乘法結果

修正符号位

原碼一位乘法（手算模拟）

&高位部分積~~~~ ~~~~低位部分積~~~~ ~~~~ ~~~~說明\\

&~~00.0000~~~~ ~~~~ ~~~~ ~~~~ 101\underline{1}|~~~~ ~~~~ 低位=1~~~~ +|x|\\

+|x|&~~00.1101~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~|\\

----&---------------------\\

&~~00.1101\\

右移&~~00.0110~~~~ ~~~~ ~~~~ ~~~~ 110\underline{1}|1~~~~ ~~~ 低位=1~~~~ +|x|\\

&~~01.0011\\

右移&~~00.1001~~~~ ~~~~ ~~~~ ~~~~ 111\underline{0}|11~~ ~~~低位=0~~~~ +0 \\

+&~~00.0000\\

&~~00.1001\\

右移&~~00.0100~~~~ ~~~~ ~~~~ ~~~~ 111\underline{1}|011 ~~~低位=1~~~~ +|x| \\

+|x|&~~00.1101\\

&~~01.0001\\

右移&~~00.1000~~~~ ~~~~ ~~~~ ~~~~ 111\underline{1}|1011 ~右移部分積和乘數全部移出 \\

&|x|=00.10001111\\

&x*y=-0.10001111\\

補碼的一位乘法

輔助位

手算模拟

&~~00.0000~~~~ ~~~~ ~~~~ 0.101\underline{1}|0~~~~ ~~~~ ~~~~起始情況\\

+[-x]_補&~~00.1101~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ Y_4Y_5=10,Y_5-Y_4=-1,+[-x]_{補}\\

----&-----------------------------\\

右移&~~00.0110~~~~ ~~~~ ~~~~ 10.10\underline{1}|10~~~~ ~~~~ ~~~~右移部分積和乘數\\

+0&~~00.0000~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ Y_4Y_5=10,Y_5-Y_4=0,+0\\

&~~00.0110\\

右移&~~00.0011~~~~ ~~~~ ~~~~ 010.1\underline{0}|110~~~~ ~~~~ ~~~~右移部分積和乘數\\

+[x]_補&~~11.0011~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ Y_4Y_5=01,Y_5-Y_4=1,+[x]_補\\

&~~11.0110\\

右移&~~11.1011~~~~ ~~~~ ~~~~ 0010.\underline{1}|0110~~~~ ~~~~ ~~~~右移部分積和乘數\\

+[-x]_補&~~00.1101~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ ~~~~ Y_4Y_5=10,Y_5-Y_4=-1,+[-x]_補\\

&~~00.1000\\

右移&~~00.0100~~~~ ~~~~ ~~~~ \underline{\underline{0001}}\underline{0}.|10110~~~~ ~~~~ ~~~~右移部分積和乘數\\

&~~11.0111\\

&[x*y]_補=11.0111~0001\\

&x*y=-0.1000~1111\\

除法運算

手算除法（十進制）

手算除法（二進制）

恢複餘數法

原碼除法：恢複餘數法

（0）初始

（1）第一步

上商

求餘數

判斷上商是否正确

01011上商後得11110，相減結果為負，應上商0

修正

邏輯左移

（2）第二步

相減結果為正數，上商正确

（3）第三步

上商無誤

（4）第四步

相減結果小于0，上商有誤

（5）第五步：最後一步除法

上商&求餘數

最後一步除法，如果上商求餘數結果小于0.還需要繼續恢複餘數

（6）最後一步

&餘數=ACC*2^{-n}\\

原碼除法（手算）

加減交替法

預設規定

被除數要小于除數，否則硬體電路無法運作，如果被除數大于除數，商的結果為大于1的數将無法表示

通過第一步的商來判斷被除數與除數的大小關系

第一步商的結果一定為負值，如果為正值說明被除數比除數大，硬體電路會立即停止運算

補碼除法

C語言中的強制類型轉換

資料的存儲和排列

大小端模式

邊界對齊

浮點數的表示

浮點數尾數的規格化

左規&右規

規格化浮點數的特點

IEEE754 浮點數标準

&IEEE754規定偏置值=2^{n-1}\\

IEEE 754 标準

&(-0.75)_{10}=(-0.11)_2=(-1.1)*2^{-1}\\

&數符=1\\

&尾數部分=.1000~0000……(隐含最高位1)\\

&階碼真值=-1\\

&單精度浮點型偏移量=127D\\

&移碼=階碼真值+偏移量=-1+111~1111=0111~1110(湊足8位)\\

浮點數的運算

浮點數的加減運算

&(0)轉換格式\\

&5D=101B,\frac{1}{256}=2^{-8},X=-101*2^-8=-0.101*2^{-5}=-0.101*2^{-101}\\

&59D=111011,\frac{1}{1024}=2^{-10},Y=111011*2^{-10}=0.111011*2^{-4}=0.111011*2^{-100}\\

&X:

&[階碼]_{原}=-101\\

&[階碼]_{補}=1011\\

&階碼雙符号位補碼：11011\\

&[尾數]_{原}=-0.101\\

&[尾數]_{補}=1.011\\

&尾數雙符号位補碼：11.011\\

&X=11011,11.011000000\\

&Y:

&[階碼]_{原}=-100\\

&[階碼]_{補}=1100\\

&階碼雙符号位補碼：11100\\

&[尾數]_{原}=0.111011\\

&[尾數]_{補}=0.111011\\

&尾數雙符号位補碼：00.111011\\

&X=11100,00.111011000\\

&浮點數加減法運算步驟\\

&(1)對階\\

&小階向大階看齊，尾數每右移一位，階碼+1\\

&[1]求階差：[\Delta E]_補=||E_X|_原+|E_Y|_補|=11011+00100=11111\\

&\Delta=-1\\

&[2]對階：X:11011,11.011000000\rightarrow 111011,11.1011000000\\

&X=-0.0101*2^{-100}\\

&(2)尾數減法\\

&-Y=11100,11.000101000\\

&11011,11.011000000\\

+&11100,11.000101000\\

---&----------------------------\\

&10.110001000\\

&X_Y=11100,10.110001000\\

&(3)規格化\\

&X_Y=11100,10.110001000\rightarrow11101,011000100\\

&(4)舍入 \\

&無需舍入\\

&(5)判斷溢出\\

&常階碼，無溢出，結果真值為2^{-3}*(-0.1001111)_2

舍入

強制類型轉換

加法器設計

算術邏輯單元ALU

機器字長=ALU一次可以處理的資料長度

計算機組成原理 第二章 資料的表示和運算