12.1目标優化
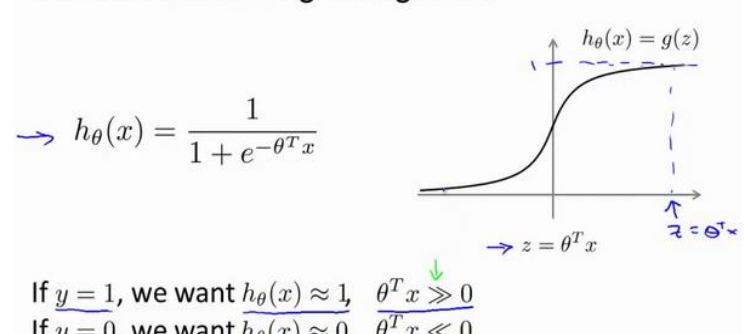
(1)以下是邏輯回歸以及單個樣本的代價函數
(2)首先将使用上圖中紫色的線(稱為cost1或者cost0)的代替曲線,然後将樣本數m去掉,最後将C代替1/λ(可以這麼了解,但不完全是),進而實作邏輯回歸的代價函數到SVM的轉換。
(3)SVM的輸出将不再是邏輯回歸的機率,而就是0或者1:
12.2大邊界的直覺了解
(1)首先對z的要求更加嚴格了,在邏輯回歸中隻要求大于或小于零,,這裡将會是大于等于1或小于等于-1。
(2)假設C非常大時,我們的優化會盡量時第一項為零,假設可以得到這樣的參數,那麼就可以将代價函數轉換為:
即在後面的限制下求解前面的最小值。
(3)C非常大時(即λ非常小),會盡量去滿足上面的限制,這樣會導緻對異常點非常敏感(過拟合),如下所示:
這時将會得到紫色的線,如果将C适當減小,會得到滿意的黑色線的。即C不那麼大時,可以忽略掉一些異常點。
(3)支援向量機經常被稱為最大間距分類器,在C很大時确實如此,但C不是那麼大時,将不是,如上一點的例子所示。但是這麼了解是有助于了解SVM的。
(4)C較大相當于λ較小,會出現過拟合;反之則出現欠拟合。
12.3數學背後的最大邊界分類(選修)
(1)向量的内積:一個向量投影到另一個向量投影長度與向量的範數的乘積,也就是對應坐标相乘再相加。
(2)目标函數要使得θ盡可能小,這時隻要使得x在θ上的投影盡可能的大,就能夠在θ取越小的值時滿足限制條件,這就是SVM背後的數學原理。
(3)θ和邊界呈現90°垂直,另外θ0為零時邊界通過原點,反之不通過原點。
12.4核函數1
(1)如果直接用多項式取拟合下面的邊界的話,肯能需要多項式的次數很高,特征很多。
(2)利用x的各個特征與我們預先標明地标(landmark)l(1),l(2),l(3),的近似程度選取新的特征f1,f2,f3。
上面是一個高斯核函數,注:這個函數與正态分布沒什麼實際上的關系,隻是看上去像而已。
(3)與地标越近結果f越接近1,越遠f越接近0。
(3)通過一下式子将很容易進行分類:
(4)核函數計算的結果即為新的特征。
12.5核函數2
(1)地标的個數設定為樣本數m,即每個樣本的位置即為地标的位置:
(2)将核函數運用到支援向量機中,
給定x,計算新特征f,當θTf>0時,預測y=1,否則反之。
相應的修改代價函數為:
在具體實施過程中,還需要對最後的正則化想微調,在計算
時,用θTMθ代替θTθ。M跟選擇的核函數有關,用相關庫幾塊使用帶核函數的SVM。
不帶核函數的SVM稱為線性核函數。
(3)以下是支援向量機的兩個參數C和σ的影響:
C=1/λ;
C較大時,相當于λ較小,可能會導緻過拟合,高方差;
C較小時,相當于λ較大,可能會導緻欠拟合,高偏差;
σ較大時,可能會導緻低方差,高偏差。
σ較小時,可能會導緻低偏差,高方差。
12.6使用支援向量機
(1)盡管不需要自己去寫SVM函數,直接使用相關庫,但需要做一下幾件事:
1.是提出參數C的選擇。在之前視訊中已經讨論了C對方差偏差的影響。
2.選擇核心參數或你想要使用的相似函數。
(2)以下是邏輯回歸和支援向量機的選擇:
1.相比于樣本數m,特征數n大的多的時候,沒有那麼多資料量去訓練一個非常複雜的模型,這時考慮用SVM。
2.如果n較小,而且m大小中等,例如n在1-1000之間,而m在10-1000之間,使用高斯函數的支援向量機。
3.如果n較小,而m較大,例如n在1-1000之間,而m大于50000,則使用支援向量機會非常慢,解決方案是創造增加更多的特征,然後使用邏輯回歸或不帶核函數的支援向量機。
神經網絡在以上三種情況下都可以有較好的表現,但神經網絡訓練可能非常慢,選擇支援向量機的原因主要在于它的代價函數是凸函數,不存在局部最小值。