R語言分段回歸資料分析案例報告

我們在這裡讨論所謂的“分段線性回歸模型”，因為它們利用包含虛拟變量的互動項。

讀取資料

data=read.csv("artificial-cover.csv")           

檢視部分資料

head(data)

##   tree.cover shurb.grass.cover
## 1       13.2              16.8
## 2       17.2              21.8
## 3       45.4              48.8
## 4       53.6              58.7
## 5       58.5              55.5
## 6       63.3              47.2           

###########用lm拟合，主要注意部分是bs（age,knots=c(...)）這部分把自變量分成不同部分
fit =lm(tree.cover~bs(shurb.grass.cover ,knots
############進行預測，預測資料也要分區
pred= predict (fit , newdata =list(shurb.grass.cover =data$shurb.grass.cover),se=T)
#############然後畫圖
plot(fit)                

可以構造一個相對複雜的 LOWESS 模型（span參數取小一些），然後和一個簡單的模型比較，如：

qplot(x, y) + geom_smooth()  # 總趨勢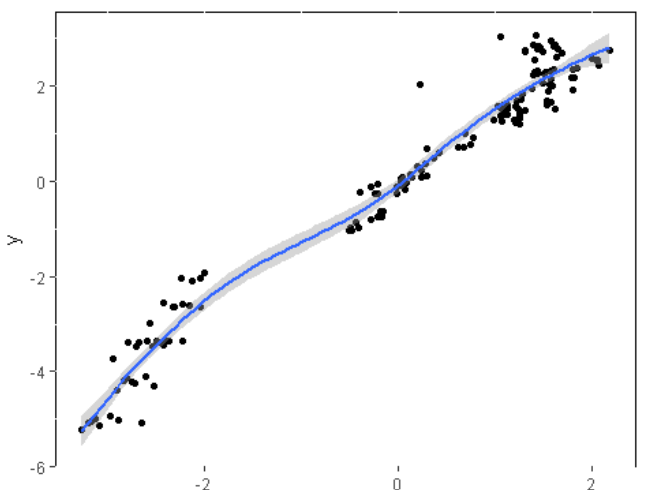           

散點圖分為兩部分

我們可以将原始散點圖分為兩部分，并拟合兩條單獨但相連的線。估計的分段式函數連接配接，在描述資料趨勢方面做得更好。

是以，讓我們為這些資料建立一個分段線性回歸模型并可視化：

0) + geom_smooth() + theme(panel.background = element_rect(fill = 'white', colour = 'black'))            

最受歡迎的見解

1.R語言多元Logistic邏輯回歸 應用案例

2.面闆平滑轉移回歸(PSTR)分析案例實作

3.matlab中的偏最小二乘回歸（PLSR）和主成分回歸（PCR）

4.R語言泊松Poisson回歸模型分析案例

5.R語言回歸中的Hosmer-Lemeshow拟合優度檢驗

6.r語言中對LASSO回歸，Ridge嶺回歸和Elastic Net模型實作

7.在R語言中實作Logistic邏輯回歸

8.python用線性回歸預測股票價格

9.R語言如何在生存分析與Cox回歸中計算IDI，NRI名額