這裡向您展示如何在R中使用glmnet包進行嶺回歸(使用L2正則化的線性回歸),并使用模拟來示範其相對于普通最小二乘回歸的優勢。
嶺回歸
當回歸模型的參數被學習時,嶺回歸使用L2正則化來權重/懲罰殘差。線上性回歸的背景下,它可以與普通最小二乘法(OLS)進行比較。OLS定義了計算參數估計值(截距和斜率)的函數。它涉及最小化平方殘差的總和。L2正則化是OLS函數的一個小增加,以特定的方式對殘差進行權重以使參數更加穩定。結果通常是一種适合訓練資料的模型,不如OLS更好,但由于它對資料中的極端變異(例如異常值)較不敏感,是以一般性更好。
包
我們将在這篇文章中使用以下軟體包:
library(tidyverse)
library(broom)
library(glmnet)
與glmnet的嶺回歸
glmnet軟體包提供了通過嶺回歸的功能glmnet()。重要的事情要知道:
它不需要接受公式和資料架構,而需要一個矢量輸入和預測器矩陣。
您必須指定alpha = 0嶺回歸。
嶺回歸涉及調整超參數lambda。glmnet()會為你生成預設值。另外,通常的做法是用lambda參數來定義你自己(我們将這樣做)。
以下是使用mtcars資料集的示例:
因為,與OLS回歸不同lm(),嶺回歸涉及調整超參數,lambda,glmnet()為不同的lambda值多次運作模型。我們可以自動找到最适合的lambda值,cv.glmnet()如下所示:
cv_fit <- cv.glmnet(x, y, alpha =0, lambda = lambdas) cv.glmnet() 使用交叉驗證來計算每個模型的概括性,我們可以将其視為:
plot(cv_fit) 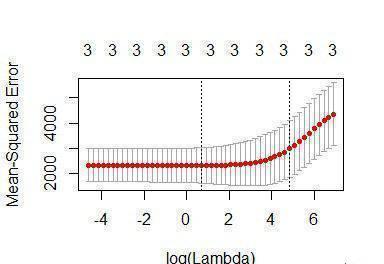
曲線中的最低點訓示最佳的lambda:最好使交叉驗證中的誤差最小化的lambda的對數值。我們可以将這個值提取為:
opt_lambda <- cv_fit$lambda.minopt_lambda
#> [1] 3.162278
我們可以通過以下方式提取所有拟合的模型(如傳回的對象glmnet()):
這是我們需要預測新資料的兩件事情。例如,預測值并計算我們訓練的資料的R 2值:
y_predicted <- predict(fit, s = opt_lambda, newx = x)
sst <- sum((y - mean(y))^2)
sse <- sum((y_predicted - y)^2)# R squared
rsq <-1- sse / sstrsq
#> [1] 0.9318896 最優模型已經在訓練資料中占93%的方差。
Ridge v OLS模拟
通過産生比OLS更穩定的參數,嶺回歸應該不太容易過度拟合訓練資料。是以,嶺回歸可能預測訓練資料不如OLS好,但更好地推廣到新資料。當訓練資料的極端變化很大時尤其如此,當樣本大小較低和/或特征的數量相對于觀察次數較多時這趨向于發生。
下面是我建立的一個模拟實驗,用于比較嶺回歸和OLS在訓練和測試資料上的預測準确性。
我首先設定了運作模拟的功能:
現在針對不同數量的訓練資料和特征的相對比例運作模拟(需要一些時間):
d <- purrr::cross_d(list(n_train = seq(20,200,20),p_features = seq(.55,.95,.05)))d <- d %>%mutate(results = map2(n_train, p_features, repeated_comparisons)) 可視化結果...
對于不同數量的訓練資料(對多個特征進行平均),兩種模型對訓練和測試資料的預測效果如何?
根據假設,OLS更适合訓練資料,但Ridge回歸更好地歸納為新的測試資料。此外,當訓練觀察次數較少時,這些影響更為明顯。
對于不同的相對特征比例(平均數量的訓練資料),兩種模型對訓練和測試資料的預測效果如何?
再一次地,OLS在訓練資料上表現稍好,但Ridge在測試資料上更好。當特征的數量相對于訓練觀察的數量相對較高時,效果更顯着。