圖結構是算法學中最強大的架構之一。
圖是各種關系的節點和邊的集合,節點是與對象對應的頂點,邊是對象之間的連接配接。
SciPy 提供了 scipy.sparse.csgraph 子產品來處理圖結構。
鄰接矩陣(Adjacency Matrix)是表示頂點之間相鄰關系的矩陣。
鄰接矩陣邏輯結構分為兩部分:V 和 E 集合,其中,V 是頂點,E 是邊,邊有時會有權重,表示節點之間的連接配接強度。
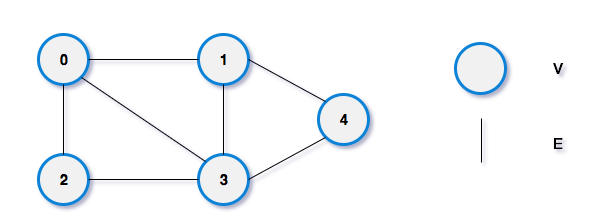
用一個一維數組存放圖中所有頂點資料,用一個二維數組存放頂點間關系(邊或弧)的資料,這個二維數組稱為鄰接矩陣。
看下下圖執行個體:
頂點有 A、B、C,邊權重有 1 和 2。
A 與 B 是連接配接的,權重為 1。
A 與 C 是連接配接的,權重為 2。
C 與 B 是沒有連接配接的。
這個鄰接矩陣可以表示為以下二維數組:
鄰接矩陣又分為有向圖鄰接矩陣和無向圖鄰接矩陣。
無向圖是雙向關系,邊沒有方向:
有向圖的邊帶有方向,是單向關系:
注:上面兩個圖中的 D 節點是自環,自環是指一條邊的兩端為同一個節點。
檢視所有連接配接元件使用 connected_components() 方法。
import numpy as np
from scipy.sparse.csgraph import connected_components
from scipy.sparse import csr_matrix
arr = np.array([
[0, 1, 2],
[1, 0, 0],
[2, 0, 0]
])
newarr = csr_matrix(arr)
print(connected_components(newarr))
以上代碼輸出結果為:
Dijkstra(迪傑斯特拉)最短路徑算法,用于計算一個節點到其他所有節點的最短路徑。
Scipy 使用 dijkstra() 方法來計算一個元素到其他元素的最短路徑。
dijkstra() 方法可以設定以下幾個參數:
return_predecessors: 布爾值,設定 True,周遊所有路徑,如果不想周遊所有路徑可以設定為 False。
indices: 元素的索引,傳回該元素的所有路徑。
limit: 路徑的最大權重。
查找元素 1 到 2 的最短路徑:
from scipy.sparse.csgraph import dijkstra
print(dijkstra(newarr, return_predecessors=True, indices=0))
弗洛伊德算法算法是解決任意兩點間的最短路徑的一種算法。
Scipy 使用 floyd_warshall() 方法來查找所有元素對之間的最短路徑。
查找所有元素對之間的最短路徑徑:
from scipy.sparse.csgraph import floyd_warshall
print(floyd_warshall(newarr, return_predecessors=True))
貝爾曼-福特算法是解決任意兩點間的最短路徑的一種算法。
Scipy 使用 bellman_ford() 方法來查找所有元素對之間的最短路徑,通常可以在任何圖中使用,包括有向圖、帶負權邊的圖。
使用負權邊的圖查找從元素 1 到元素 2 的最短路徑:
from scipy.sparse.csgraph import bellman_ford
[0, -1, 2],
print(bellman_ford(newarr, return_predecessors=True, indices=0))
depth_first_order() 方法從一個節點傳回深度優先周遊的順序。
可以接收以下參數:
圖
圖開始周遊的元素
給定一個鄰接矩陣,傳回深度優先周遊的順序:
from scipy.sparse.csgraph import depth_first_order
[0, 1, 0, 1],
[1, 1, 1, 1],
[2, 1, 1, 0],
[0, 1, 0, 1]
print(depth_first_order(newarr, 1))
breadth_first_order() 方法從一個節點傳回廣度優先周遊的順序。
給定一個鄰接矩陣,傳回廣度優先周遊的順序:
from scipy.sparse.csgraph import breadth_first_order
print(breadth_first_order(newarr, 1))