空間資料又稱幾何資料,它用來表示物體的位置、形态、大小分布等各方面的資訊,比如坐标上的點。
SciPy 通過 scipy.spatial 子產品處理空間資料,比如判斷一個點是否在邊界内、計算給定點周圍距離最近點以及給定距離内的所有點。
三角測量在三角學與幾何學上是一借由測量目标點與固定基準線的已知端點的角度,測量目标距離的方法。
多邊形的三角測量是将多邊形分成多個三角形,我們可以用這些三角形來計算多邊形的面積。
拓撲學的一個已知事實告訴我們:任何曲面都存在三角剖分。
假設曲面上有一個三角剖分, 我們把所有三角形的頂點總個數記為 p(公共頂點隻看成一個),邊數記為 a,三角形的個數記為 n,則 e=p-a+n 是曲面的拓撲不變量。 也就是說不管是什麼剖分,e 總是得到相同的數值。 e 被稱為稱為歐拉示性數。
對一系列的點進行三角剖分點方法是 Delaunay() 三角剖分。
通過給定的點來建立三角形:
import numpy as np
from scipy.spatial import Delaunay
import matplotlib.pyplot as plt
points = np.array([
[2, 4],
[3, 4],
[3, 0],
[2, 2],
[4, 1]
])
simplices = Delaunay(points).simplices # 三角形中頂點的索引
plt.triplot(points[:, 0], points[:, 1], simplices)
plt.scatter(points[:, 0], points[:, 1], color='r')
plt.show()
輸出結果如下圖所示:
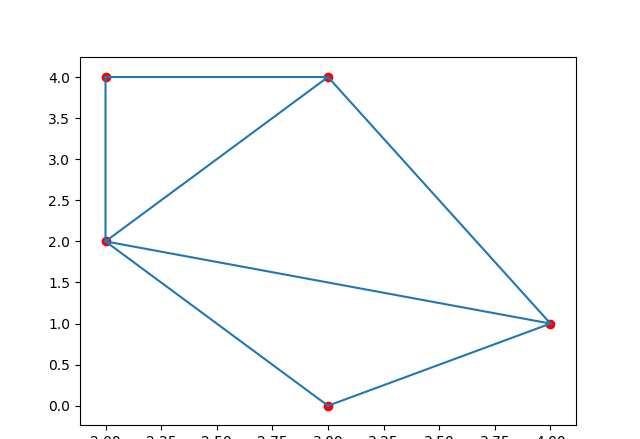
注:三角形頂點的 id 存儲在三角剖分對象的 simplices 屬性中。
凸包(Convex Hull)是一個計算幾何(圖形學)中的概念。
在一個實數向量空間 V 中,對于給定集合 X,所有包含 X 的凸集的交集 S 被稱為 X 的凸包。X 的凸包可以用 X 内所有點(X1,...Xn)的凸組合來構造。
我們可以使用 ConvexHull() 方法來建立凸包。
通過給定的點來建立凸包:
from scipy.spatial import ConvexHull
[4, 1],
[1, 2],
[5, 0],
[3, 1],
[0, 2]
hull = ConvexHull(points)
hull_points = hull.simplices
plt.scatter(points[:,0], points[:,1])
for simplex in hull_points:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
kd-tree(k-dimensional樹的簡稱),是一種對k維空間中的執行個體點進行存儲以便對其進行快速檢索的樹形資料結構。主要應用于多元空間關鍵資料的搜尋(如:範圍搜尋和最近鄰搜尋)。
K-D 樹可以使用在多種應用場合,如多元鍵值搜尋(範圍搜尋及最鄰近搜尋)。
最鄰近搜尋用來找出在樹中與輸入點最接近的點。
KDTree() 方法傳回一個 KDTree 對象。
query() 方法傳回最鄰近距離和最鄰近位置。
查找到 (1,1) 的最鄰近距離:
from scipy.spatial import KDTree
points = [(1, -1), (2, 3), (-2, 3), (2, -3)]
kdtree = KDTree(points)
res = kdtree.query((1, 1))
print(res)
在數學中, 一個距離矩陣是一個各項元素為點之間距離的矩陣(二維數組)。是以給定 N 個歐幾裡得空間中的點,其距離矩陣就是一個非負實數作為元素的 N×N 的對稱矩陣距離矩陣和鄰接矩陣概念相似,其差別在于後者僅包含元素(點)之間是否有連邊,并沒有包含元素(點)之間的連通的距離的訊息。是以,距離矩陣可以看成是鄰接矩陣的權重形式。
舉例來說,我們分析如下二維點 a 至 f。在這裡,我們把點所在像素之間的歐幾裡得度量作為距離度量。
其距離矩陣為:
距離矩陣的這些資料可以進一步被看成是圖形表示的熱度圖(如下圖所示),其中黑色代表距離為零,白色代表最大距離。
在生物資訊學中,距離矩陣用來表示與坐标系無關的蛋白質結構,還有序列空間中兩個序列之間的距離。這些表示被用在結構比對,序列比對,還有在核磁共振,X射線和結晶學中确定蛋白質結構。
在數學中,歐幾裡得距離或歐幾裡得度量是歐幾裡得空間中兩點間"普通"(即直線)距離。使用這個距離,歐氏空間成為度量空間。相關聯的範數稱為歐幾裡得範數。較早的文獻稱之為畢達哥拉斯度量。
歐幾裡得度量(euclidean metric)(也稱歐氏距離)是一個通常采用的距離定義,指在m維空間中兩個點之間的真實距離,或者向量的自然長度(即該點到原點的距離)。在二維和三維空間中的歐氏距離就是兩點之間的實際距離。
以下執行個體檢視給定點之間的歐幾裡德距離:
from scipy.spatial.distance import euclidean
p1 = (1, 0)
p2 = (10, 2)
res = euclidean(p1, p2)
計程車幾何或曼哈頓距離(Manhattan Distance)是由十九世紀的赫爾曼·闵可夫斯基所創詞彙 ,是種使用在幾何度量空間的幾何學用語,用以标明兩個點在标準坐标系上的絕對軸距總和。
曼哈頓距離 隻能上、下、左、右四個方向進行移動,并且兩點之間的曼哈頓距離是兩點之間的最短距離。
曼哈頓與歐幾裡得距離: 紅、藍與黃線分别表示所有曼哈頓距離都擁有一樣長度(12),而綠線表示歐幾裡得距離有6×√2 ≈ 8.48的長度。
以下執行個體通過給點的點計算曼哈頓距離:
from scipy.spatial.distance import cityblock
res = cityblock(p1, p2)
輸出結果為:
餘弦距離,也稱為餘弦相似度,通過測量兩個向量的夾角的餘弦值來度量它們之間的相似性。
0 度角的餘弦值是 1,而其他任何角度的餘弦值都不大于 1,并且其最小值是 -1。
以下執行個體計算 A 與 B 兩點的餘弦距離:
from scipy.spatial.distance import cosine
res = cosine(p1, p2)
在資訊論中,兩個等長字元串之間的漢明距離(英語:Hamming distance)是兩個字元串對應位置的不同字元的個數。換句話說,它就是将一個字元串變換成另外一個字元串所需要替換的字元個數。
漢明重量是字元串相對于同樣長度的零字元串的漢明距離,也就是說,它是字元串中非零的元素個數:對于二進制字元串來說,就是 1 的個數,是以 11101 的漢明重量是 4。
<b>1011101</b>與<b>1001001</b>之間的漢明距離是2。
<b>2143896</b>與<b>2233796</b>之間的漢明距離是3。
"<b>toned</b>"與"<b>roses</b>"之間的漢明距離是3。
以下執行個體計算兩個點之間的漢明距離:
from scipy.spatial.distance import hamming
p1 = (True, False, True)
p2 = (False, True, True)
res = hamming(p1, p2)