图结构是算法学中最强大的框架之一。
图是各种关系的节点和边的集合,节点是与对象对应的顶点,边是对象之间的连接。
SciPy 提供了 scipy.sparse.csgraph 模块来处理图结构。
邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。
邻接矩阵逻辑结构分为两部分:V 和 E 集合,其中,V 是顶点,E 是边,边有时会有权重,表示节点之间的连接强度。
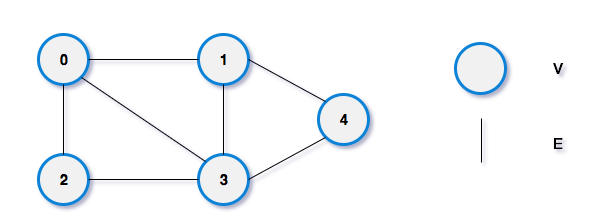
用一个一维数组存放图中所有顶点数据,用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。
看下下图实例:
顶点有 A、B、C,边权重有 1 和 2。
A 与 B 是连接的,权重为 1。
A 与 C 是连接的,权重为 2。
C 与 B 是没有连接的。
这个邻接矩阵可以表示为以下二维数组:
邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。
无向图是双向关系,边没有方向:
有向图的边带有方向,是单向关系:
注:上面两个图中的 D 节点是自环,自环是指一条边的两端为同一个节点。
查看所有连接组件使用 connected_components() 方法。
import numpy as np
from scipy.sparse.csgraph import connected_components
from scipy.sparse import csr_matrix
arr = np.array([
[0, 1, 2],
[1, 0, 0],
[2, 0, 0]
])
newarr = csr_matrix(arr)
print(connected_components(newarr))
以上代码输出结果为:
Dijkstra(迪杰斯特拉)最短路径算法,用于计算一个节点到其他所有节点的最短路径。
Scipy 使用 dijkstra() 方法来计算一个元素到其他元素的最短路径。
dijkstra() 方法可以设置以下几个参数:
return_predecessors: 布尔值,设置 True,遍历所有路径,如果不想遍历所有路径可以设置为 False。
indices: 元素的索引,返回该元素的所有路径。
limit: 路径的最大权重。
查找元素 1 到 2 的最短路径:
from scipy.sparse.csgraph import dijkstra
print(dijkstra(newarr, return_predecessors=True, indices=0))
弗洛伊德算法算法是解决任意两点间的最短路径的一种算法。
Scipy 使用 floyd_warshall() 方法来查找所有元素对之间的最短路径。
查找所有元素对之间的最短路径径:
from scipy.sparse.csgraph import floyd_warshall
print(floyd_warshall(newarr, return_predecessors=True))
贝尔曼-福特算法是解决任意两点间的最短路径的一种算法。
Scipy 使用 bellman_ford() 方法来查找所有元素对之间的最短路径,通常可以在任何图中使用,包括有向图、带负权边的图。
使用负权边的图查找从元素 1 到元素 2 的最短路径:
from scipy.sparse.csgraph import bellman_ford
[0, -1, 2],
print(bellman_ford(newarr, return_predecessors=True, indices=0))
depth_first_order() 方法从一个节点返回深度优先遍历的顺序。
可以接收以下参数:
图
图开始遍历的元素
给定一个邻接矩阵,返回深度优先遍历的顺序:
from scipy.sparse.csgraph import depth_first_order
[0, 1, 0, 1],
[1, 1, 1, 1],
[2, 1, 1, 0],
[0, 1, 0, 1]
print(depth_first_order(newarr, 1))
breadth_first_order() 方法从一个节点返回广度优先遍历的顺序。
给定一个邻接矩阵,返回广度优先遍历的顺序:
from scipy.sparse.csgraph import breadth_first_order
print(breadth_first_order(newarr, 1))