幾何深度學習是一個非常令人興奮的新領域,但它的數學正在慢慢地進入代數拓撲和理論實體領域。
本文使用規範理論的語言,它處于實體學中任何喜歡同時使用"量子"和"場"這兩個詞的中心。它有望直覺地了解規範理論的基礎知識。
我想在這裡做的是給出純粹直覺的了解,沒有數學。
在下文中,我将假設你知道卷積神經網絡(CNN)是如何工作的,但不知道它們與流形有什麼關系。
流形
一個流形是一件簡單的事情。你看到的每個二維表面都可以被認為是一個流形。球體表面,立方體表面,所有流形。但它不僅限于二維,哎呀,它甚至不限于可以想象的東西。曲線是一種流形。4-D時空是一個多方面。它很一般,描述了一個空間。但是讓我們關注二維表面。最簡單的表面是平面,例如計算機螢幕。當我們與CNN進行卷積時,我們通常會在這些平面圖像上進行卷積。
比方說,我們想用CNN來預測天氣。對于一個國家,這很容易:使用當地的天氣資料作為輸入和keras-keras-boom,你有一個訓練有素的模型。如果我們想對整個星球的天氣進行分類怎麼辦?你如何将它融入單個圖像?
但有一個問題。實際上,左邊和右邊是相同的位置。此外,整個頂部邊緣對應于單個點,下邊緣也是如此。整件事都是扭曲的。曾經試過壓扁乒乓球嗎?是的,那不順利。當我們嘗試應用卷積時,我們會得到奇怪的結果。不實際的事情可能發生在邊緣。它可以預測圖像最右側的強烈東風,但圖像左側沒有任何東西,即使它們代表相同的位置。CNN隻是不明白地球環繞。
或者,我們可以為地球建立多個重疊地圖,并擁有對其進行操作的CNN。這組地圖也稱為地圖集。在所有這些單獨的地圖上移動 CNN,確定在它們重疊的同一點上繼續在下一個地圖上,然後應該使它能夠了解地球是圓的。這是幾何深度學習背後的基本思想:直接将深度學習應用于曲面或流形以保持其幾何結構。
去新加坡
現在,讓我們忘記一秒鐘的天氣并取出指南針。假設你在新加坡。向北,經過泰國,經過中國,蒙古到達北極。并且不改變方向,繼續前進。你要經過加拿大,美國,直到你到達中美洲的某個地方。停在那裡,開始在太平洋遊泳,不改變方向!幾百萬招後,你應該回到新加坡。可是等等。你從來沒有改變方向,你為什麼要向南看?
讓我們再說一遍,但是這次我們到達北極時我們會向左側走。我們最終會在尼日拉附近開始向後走,再也不會改變我們的方向。一旦我們回到新加坡,這次我們向西看?奇怪......别相信我?自己嘗試一下,隻需拿一個指南針開始遊泳......
這個問題是由于球體的曲率造成的,我們稱之為"在不改變方向的情況下移動"作為平行傳輸。你看到并行傳輸非常依賴于球體上的路徑。然而,在二維飛機上,無關緊要。一旦你回來,你可以走在每條路徑而不改變方向,并有相同的方向。是以,我們說平面是可并行化的(一旦你回來你的方向向量保持平行),而球體不是。
你可以看到這對我們在球體上的CNN來說是一個問題。如果我們以不同的方式将CNN轉移到我們所有的地圖上,那麼方向似乎會改變。我們需要找到一種方法來確定這種古怪不會影響我們的結果!或者,至少我們應該知道如何處理它。
毛茸茸的毛球
在找到解決方案之前,我們必須引入更多的數學概念。指南針可以被視為指向某個方向的飛機上的矢量,主要是北方。針旋轉的這個平面與地球表面相切,我們将它稱為地球在這個地方的切線空間。即使地球是圓的,切線空間也是完全平坦的。它的作用就像一個局部坐标系,北面和東面是它的坐标向量。而且,由于我們可以在地球上的任何地方取出指南針,每個地點都有自己的切線空間。但我們也可以将40°和130°定義為我們的坐标向量。北方和其他方向在這種情況下并不特别,選擇是任意的。
現在,讓我們選擇切線空間中的任何方向,然後向前邁進一小步。我們確定采用最短的路徑(測地線)并最終達到一個新的點。你可以稱之為"前進",但是為了讓每個人感到困惑,我們将這個過程稱為指數映射(這是因為所有這些微小步驟神奇地類似于指數函數的系列擴充......但現在這并不重要) 。
讓我們再看看我們的指南針。羅盤将矢量配置設定給地球上的"每個"點的事實稱為(切線)矢量場。風也可以看作矢量場,因為它為每個點指定方向。當你直接站在磁北或磁南時,我特意将"每一個"放在引号中,因為羅盤針出了問題。事實上,對于球體上的每個非零連續矢量場都是錯誤的。我們必須在球體上的磁場中有極點。這種現象被稱為毛球定理,因為它類似于無法梳理毛球,而不會産生旋轉:
矢量場不需要與切線空間具有相同的尺寸。相反,它們可以在每個點上擁有自己的任意次元的向量空間。這很重要,因為我們還希望能夠為地球上的每個點配置設定3-D或99-D矢量而不僅僅是2-D方向。在場的每個點處的該向量空間也被稱為光纖。
(一種特殊類型的場是标量場。它隻有一個次元,溫度可以看作是這樣一個标量場)
規
各地的溫度測量方法不同。在德國,我們使用Celsius。在美國,他們使用華氏溫度。這種選擇稱為量規。是的,這個詞來自測量儀器。現在,當我從美國讀到天氣預報時,我必須計算出華氏溫度在攝氏溫度下的含義。我們有不同的參考架構。該計算稱為規範變換。請注意,實際溫度沒有變化,隻是我們用來了解它的值,變換是一個簡單的線性函數。
如果我們看一下矢量場,比如風向,事情會變得更加複雜。為了達到極限,讓我們假裝一些國家,Gaugeland,它并不真正關心北方和南方,并且有自己的方向系統,基于星座或刺猬恐懼時的方向。當這些人描述風時,我們必須進行規範轉換以了解他們所談論的方向。現在,規範變換成為可逆矩陣的乘法(它必須明顯地兩種方式)。這一組矩陣的被稱為 的一般線性群或GL。
對于理論上的扁平地球,風的選擇可以是全局的。但在一個領域,我們遇到了問題。我們無法定義單個全局儀表,但必須依賴多個儀表和地圖。根據我們在球體上的并行化問題和毛球定理,我們應該有一些直覺,為什麼必須如此。
這自動意味着我們需要多個風圖。然而,我們不再允許所有Gaugeland的shenaniganz,并要求至少他們使用的矢量(風速)的幅度必須與我們的相同。我們隻允許他們使用不同的方向。是以,每個規格變換減少為旋轉。這些變換也形成一組,即特殊正交組或SO,它是GL的子組。通過選擇不同的結構組,我們有效地減少了我們的規範理論可能具有的允許變換。
回到深度學習
我們回到原來的問題,想要在風向矢量場上進行卷積。這裡,風代表輸入特征。假設我們想要找龍卷風方向作為輸出。我們可以對"小更新檔"執行卷積以從風向提取這些輸出特征。(注意:我不知道這是否具有氣象意義......輸出向量到輸出向量......這就是我們需要知道的全部)
但"小更新檔"是一個非常模糊的描述。在二維平面上,它是直截了當的,我們可以把一些球内的所有東西都放在更新檔的中心周圍。這在某種程度上也适用于完美的球體。但在任意多方面?事情變得棘手。看看這個時髦的流形:
它被稱為Klein瓶,我們可以看到,點之間的原始距離是......有問題的。我們可能永遠不會需要Klein瓶進行深度學習,但我們希望盡可能保持一般性。
我們需要的是在拓撲意義上僅包括在流形附近的卷積中的點的方法。我們确實有辦法做到這一點。回想一下,指數圖在我們的流形上做了微小的步驟來找到附近的點。是以讓我們用它。從中心開始,我們向切線空間允許的每個方向邁出一步,并将這一點包含在我們的卷積中。
我們現在需要的是一些與卷積相關的函數。是以,我們定義了一個核心,為每個指針配置設定一個矩陣......等待,不,我們用指數映射的切線空間的每個方向。這有點奇怪,但是當你看到經典的2-D卷積時,它實際上也是如此。它不是那麼明顯,因為它在飛機上。
該矩陣乘以輸入矢量并産生輸出矢量。在這裡,作者确定了第一個問題。該矩陣僅針對中心定義。但是我們将它應用于附近點的場矢量,它們有自己奇怪的屬性。在一個平面上,這不是問題,但在我們的領域,它們略有不同,我們不能隻應用核心。
讓我們解決這個問題并将這些點上的向量傳輸回我們小更新檔的中心。在這裡,我們可以應用我們的矩陣,而不必擔心奇怪的曲率問題。
Gauge Equivariance
到目前為止我們定義的卷積似乎是明智的。我們應用我們的核心來擷取資料并得到一個很好的結果:龍卷風向東移動。但不知何故,與Gaugeland相比,我們仍然得到不同的結果?他們預測龍卷風正在移動刺猬左派?
啊,是的:我們需要衡量将他們的結果轉化為我們的架構aaa和voila:他們預測龍卷風會向西走。還是錯的......
發生了什麼?我們忘了讓我們的卷積規範變得相同。簡而言之,核心的結果必須依賴于所選擇的規格并且等效地變換。如果沒有,我們隻會得到無法互相關聯或互相比較的奇怪結果。
但是輸出矢量可能是一個不同的次元,或者與輸入有不同的解釋,我們如何将輸入的規範變換與輸出的等變"規範變換"聯系起來?那麼,作為結構組隻作用于輸入,這個想法是要找到一個表示作用在輸出向量相同的基團。
例如,具有旋轉組作為其結構組的2-D輸入矢量的變換可以由圍繞單個軸旋轉的3-D輸出矢量表示。當2-D矢量旋轉時,3-D輸出也圍繞固定軸旋轉。通常,可以存在許多表示,例如在3D中可以存在許多不同的旋轉軸。關鍵是,它做了代表相同動作的事情。
有了表示的概念,我們可以使卷積規範變得相同。我們隻需要確定輸入向量的規範變換導緻輸出向量的等變變換(即,相同的變換,但在适當的表示中)。
現在,使用規範等效,當我們在不同的地圖上執行卷積時,我們得到不同的結果,但它們對于該特定地圖是有意義的。這是我們定義卷積以在整個範圍内有意義的最佳方式。
二十面體?
我們基本上涵蓋了論文的第2部分。作者現在轉向二十面體,它與拓撲結構非常相似,但更好。它們更好,我們可以比球體更容易離散它們。
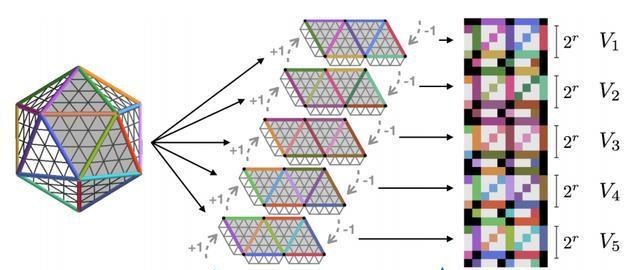
就像我們用多個地圖覆寫地球時一樣,讓我們用五個重疊的地圖覆寫二十面體(重疊用小的全白三角形表示):

美麗,地圖甚至大小相同。難怪他們選擇了這種多樣性。我們也可以将其視為圖表。注意,每個節點,即每個交叉點,是具有輸入特征向量的歧管上的點(在上圖中不可見)。每個小三角形都有3個角,每個角都是這些節點之一。他們是我們感興趣的。
那麼,讓我們做卷積!
首先,我們需要看看我們的指數地圖是什麼樣的。好吧,在我們的離散歧管上,這很容易。我們隻是從節點開始向任何方向邁出一步。方向在上圖中可見為連接配接節點的線。是以,大多數節點有6個鄰居,除了在二十面體的角落有5個鄰居。
接下來,我們需要一個核心函數。但我們很懶,不想重新發明輪子。是以,我們隻使用标準2D卷積的3 x 3濾波器。這些3 x 3濾波器具有中心點和8個鄰居。這比我們需要的還要多。是以,讓我們忽略3 x 3網格中的右上角和左下角鄰居,并假裝它隻有6個鄰居。
剩下的就是讓這個東西變得規範。那麼,讓我們來看看我們的二十面體的結構組。我們已經注意到,我們隻能進入6個不同的方向。如果我們在這個結構上描述風,我們将隻有6個不同的離散風向。是以,我們的儀表變換限于60°旋轉,其也可以表示為6階或C6的循環群。
最後,我提到我們的地圖是重疊的。是以,如果我們想要在具有重疊的區域上移動卷積濾波器,我們基本上使用來自不同映射的值。我們如何處理這些價值觀?在我們使用它們之前,我們會測量它們到正确的幀。瞧,我們正在對二十面體進行卷積。
結論
在我看來,本文為幾何深度學習領域提供了基本的結果。在進行卷積時了解儀表等效性的總體思路和重要性是這裡的主要内容。