5.13
A.
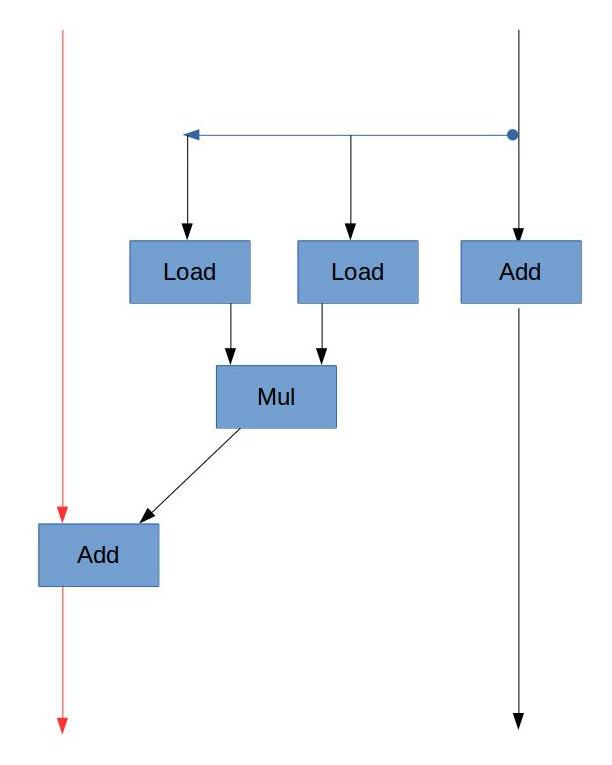
B. 由浮點數加法的延遲,CPE的下界應該是3。
C. 由整數加法的延遲,CPE的下界應該是1.
D. 由A中的資料流圖,雖然浮點數乘法需要5個周期,但是它沒有“資料依賴”,也就是說,每次循環時的乘法不需要依賴上一次乘法的結果,可以各自獨立進行。但是加法是依賴于上一次的結果的(sum = sum + 乘法結果),是以該循環的“關鍵路徑”是加法這條鍊。而浮點數加法的延遲為3個周期,是以CPE為3.00。
5.14
A. 由5.13中分析的,關鍵路徑是一個加法,而整數加法的延遲為1個周期,是以CPE的下界為1。
更新:題意弄錯,不是隻分析6*1整數運算,跳跳熊12138指出,已更正。
下面是跳跳熊12138給的答案:
本題的代碼有n(資料規模)次加運算和乘運算。cpe最低的情況是加的功能功能單元和乘的功能單元全都處于滿流水的狀态,此時加和乘都達到吞吐量下界。對于整數運算,加法的吞吐量下界為0.5,乘法的吞吐量下界為1.0,是以cpe=max{0.5,1.0};對于浮點數運算,加法的吞吐量下界是1.0,乘法的吞吐量下界是0.5,是以cpe=max{1.0,0.5}=1.0。綜上,cpe的下界是1.0。
B. “6 * 1 loop unrolling”隻減少了循環的次數(是以整數的CPE下降了,書上把這個稱為“overhead”),并沒有減少記憶體讀寫的次數和流水線的發生,是以浮點數運算還是不能突破“關鍵路徑”的CPE下界。
5.15
雖然此時可以流水線,但是浮點數加法的單元的Issue time為1個周期,而Capacity也為1,是以最多每個時鐘周期完成I/C = 1個加法操作,即此時CPE的下界為1。
5.16
5.17
5.18
答案不唯一,我這裡是利用10 × 10的loop unrolling改“direct evaluation”的版本。
原函數的瓶頸在于<code>xpwr = xpwr * x</code>這一句,乘法資料依賴,由書上給出的<code>K >= L*C</code> (第540面),其中L是latency,C是capacity,由于浮點數乘法分别對應5和2,是以這裡的K選擇為10。
另外,K大的時候很可能會碰到寄存器不夠的情況,不得不使用棧來儲存局部變量(運作的時候會加載到高速緩存),會有一些性能上的犧牲。
5.19
瓶頸在于<code>val=val+a[i]</code> (書上還加了<code>last_val</code> ,一個意思)這一句,加法資料依賴,由書上給出的<code>K >= L*C</code> (第540面),其中L是latency,C是capacity,由于浮點數加法分别對應3和1,是以這裡選擇3*1a。