5.13
A.
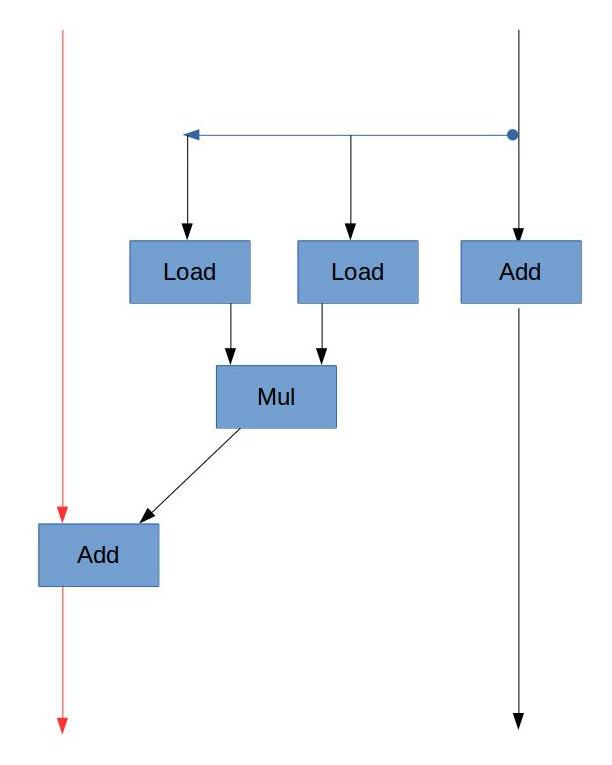
B. 由浮点数加法的延迟,CPE的下界应该是3。
C. 由整数加法的延迟,CPE的下界应该是1.
D. 由A中的数据流图,虽然浮点数乘法需要5个周期,但是它没有“数据依赖”,也就是说,每次循环时的乘法不需要依赖上一次乘法的结果,可以各自独立进行。但是加法是依赖于上一次的结果的(sum = sum + 乘法结果),所以该循环的“关键路径”是加法这条链。而浮点数加法的延迟为3个周期,所以CPE为3.00。
5.14
A. 由5.13中分析的,关键路径是一个加法,而整数加法的延迟为1个周期,所以CPE的下界为1。
更新:题意弄错,不是只分析6*1整数运算,跳跳熊12138指出,已更正。
下面是跳跳熊12138给的答案:
本题的代码有n(数据规模)次加运算和乘运算。cpe最低的情况是加的功能功能单元和乘的功能单元全都处于满流水的状态,此时加和乘都达到吞吐量下界。对于整数运算,加法的吞吐量下界为0.5,乘法的吞吐量下界为1.0,所以cpe=max{0.5,1.0};对于浮点数运算,加法的吞吐量下界是1.0,乘法的吞吐量下界是0.5,所以cpe=max{1.0,0.5}=1.0。综上,cpe的下界是1.0。
B. “6 * 1 loop unrolling”只减少了循环的次数(所以整数的CPE下降了,书上把这个称为“overhead”),并没有减少内存读写的次数和流水线的发生,所以浮点数运算还是不能突破“关键路径”的CPE下界。
5.15
虽然此时可以流水线,但是浮点数加法的单元的Issue time为1个周期,而Capacity也为1,所以最多每个时钟周期完成I/C = 1个加法操作,即此时CPE的下界为1。
5.16
5.17
5.18
答案不唯一,我这里是利用10 × 10的loop unrolling改“direct evaluation”的版本。
原函数的瓶颈在于<code>xpwr = xpwr * x</code>这一句,乘法数据依赖,由书上给出的<code>K >= L*C</code> (第540面),其中L是latency,C是capacity,由于浮点数乘法分别对应5和2,所以这里的K选择为10。
另外,K大的时候很可能会碰到寄存器不够的情况,不得不使用栈来保存局部变量(运行的时候会加载到高速缓存),会有一些性能上的牺牲。
5.19
瓶颈在于<code>val=val+a[i]</code> (书上还加了<code>last_val</code> ,一个意思)这一句,加法数据依赖,由书上给出的<code>K >= L*C</code> (第540面),其中L是latency,C是capacity,由于浮点数加法分别对应3和1,所以这里选择3*1a。